bigint.h File Reference

#include "amath.h"

Include dependency graph for bigint.h:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Classes
struct	BigInt

Enumerations
enum	tCutoffMode { CutoffMode_Unique, CutoffMode_TotalLength, CutoffMode_FractionLength }

Functions
uint32_t	Dragon4 (uint64_t mantissa, int32_t exponent, uint32_t mantissaHighBitIdx, bool hasUnequalMargins, tCutoffMode cutoffMode, uint32_t cutoffNumber, char *pOubooluffer, uint32_t bufferSize, int32_t *pOutExponent)

Variables
const uint32_t	c_BigInt_MaxBlocks = 35

Enumeration Type Documentation

tCutoffMode

enum tCutoffMode

Enumerator
CutoffMode_Unique
CutoffMode_TotalLength
CutoffMode_FractionLength

Definition at line 120 of file bigint.h.

{
    CutoffMode_Unique,         // as many digits as necessary to print a uniquely identifiable number
    CutoffMode_TotalLength,    // up to cutoffNumber significant digits
    CutoffMode_FractionLength, // up to cutoffNumber significant digits past the decimal point
};

Function Documentation

Dragon4()

uint32_t Dragon4	(	uint64_t	mantissa,
		int32_t	exponent,
		uint32_t	mantissaHighBitIdx,
		bool	hasUnequalMargins,
		tCutoffMode	cutoffMode,
		uint32_t	cutoffNumber,
		char *	pOubooluffer,
		uint32_t	bufferSize,
		int32_t *	pOutExponent
	)

Definition at line 608 of file bigint.cpp.

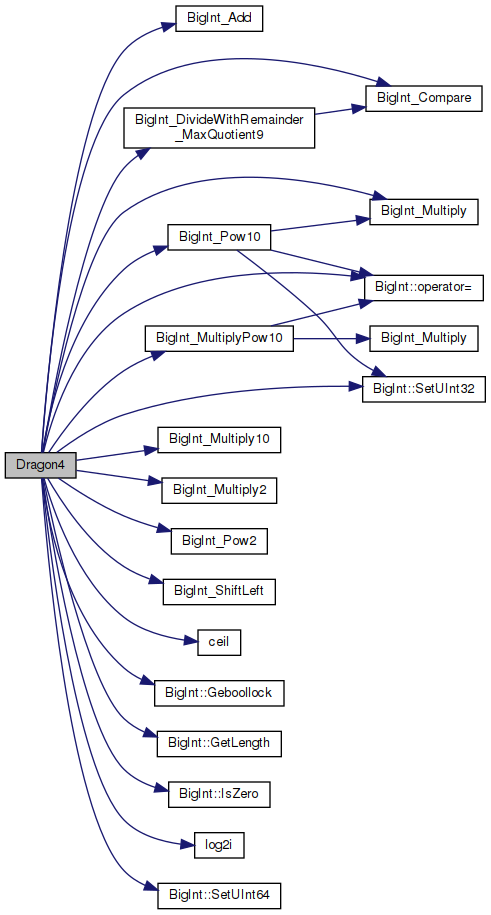
References BigInt_Add(), BigInt_Compare(), BigInt_DivideWithRemainder_MaxQuotient9(), BigInt_Multiply(), BigInt_Multiply10(), BigInt_Multiply2(), BigInt_MultiplyPow10(), BigInt_Pow10(), BigInt_Pow2(), BigInt_ShiftLeft(), ceil(), CutoffMode_FractionLength, CutoffMode_TotalLength, CutoffMode_Unique, BigInt::Geboollock(), BigInt::GetLength(), BigInt::IsZero(), log2i(), BigInt::operator=(), BigInt::SetUInt32(), and BigInt::SetUInt64().

Referenced by DecimalSystem::GetText().

{
    char *pCurDigit = pOubooluffer;

    assert(bufferSize > 0);

    // if the mantissa is zero, the value is zero regardless of the exponent
    if (mantissa == 0)
    {
        *pCurDigit = '0';
        *pOutExponent = 0;
        return 1;
    }

    // compute the initial state in integral form such that
    //  value     = scaledValue / scale
    //  marginLow = scaledMarginLow / scale
    BigInt scale;           // positive scale applied to value and margin such that they can be
                            //  represented as whole numbers
    BigInt scaledValue;     // scale * mantissa
    BigInt scaledMarginLow; // scale * 0.5 * (distance between this floating-point number and its
                            //  immediate lower value)

    // For normalized IEEE floating point values, each time the exponent is incremented the margin also
    // doubles. That creates a subset of transition numbers where the high margin is twice the size of
    // the low margin.
    BigInt *pScaledMarginHigh;
    BigInt optionalMarginHigh;

    if (hasUnequalMargins)
    {
        // if we have no fractional component
        if (exponent > 0)
        {
            // 1) Expand the input value by multiplying out the mantissa and exponent. This represents
            //    the input value in its whole number representation.
            // 2) Apply an additional scale of 2 such that later comparisons against the margin values
            //    are simplified.
            // 3) Set the margin value to the lowest mantissa bit's scale.

            // scaledValue      = 2 * 2 * mantissa*2^exponent
            scaledValue.SetUInt64(4 * mantissa);
            BigInt_ShiftLeft(&scaledValue, exponent);

            // scale            = 2 * 2 * 1
            scale.SetUInt32(4);

            // scaledMarginLow  = 2 * 2^(exponent-1)
            BigInt_Pow2(&scaledMarginLow, exponent);

            // scaledMarginHigh = 2 * 2 * 2^(exponent-1)
            BigInt_Pow2(&optionalMarginHigh, exponent + 1);
        }
        // else we have a fractional exponent
        else
        {
            // In order to track the mantissa data as an integer, we store it as is with a large scale

            // scaledValue      = 2 * 2 * mantissa
            scaledValue.SetUInt64(4 * mantissa);

            // scale            = 2 * 2 * 2^(-exponent)
            BigInt_Pow2(&scale, -exponent + 2);

            // scaledMarginLow  = 2 * 2^(-1)
            scaledMarginLow.SetUInt32(1);

            // scaledMarginHigh = 2 * 2 * 2^(-1)
            optionalMarginHigh.SetUInt32(2);
        }

        // the high and low margins are different
        pScaledMarginHigh = &optionalMarginHigh;
    }
    else
    {
        // if we have no fractional component
        if (exponent > 0)
        {
            // 1) Expand the input value by multiplying out the mantissa and exponent. This represents
            //    the input value in its whole number representation.
            // 2) Apply an additional scale of 2 such that later comparisons against the margin values
            //    are simplified.
            // 3) Set the margin value to the lowest mantissa bit's scale.

            // scaledValue     = 2 * mantissa*2^exponent
            scaledValue.SetUInt64(2 * mantissa);
            BigInt_ShiftLeft(&scaledValue, exponent);

            // scale           = 2 * 1
            scale.SetUInt32(2);

            // scaledMarginLow = 2 * 2^(exponent-1)
            BigInt_Pow2(&scaledMarginLow, exponent);
        }
        // else we have a fractional exponent
        else
        {
            // In order to track the mantissa data as an integer, we store it as is with a large scale

            // scaledValue     = 2 * mantissa
            scaledValue.SetUInt64(2 * mantissa);

            // scale           = 2 * 2^(-exponent)
            BigInt_Pow2(&scale, -exponent + 1);

            // scaledMarginLow = 2 * 2^(-1)
            scaledMarginLow.SetUInt32(1);
        }

        // the high and low margins are equal
        pScaledMarginHigh = &scaledMarginLow;
    }

    // Compute an estimate for digitExponent that will be correct or undershoot by one.
    // This optimization is based on the paper "Printing Floating-Point Numbers Quickly and Accurately"
    // by Burger and Dybvig http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.72.4656&rep=rep1&type=pdf
    // We perform an additional subtraction of 0.69 to increase the frequency of a failed estimate
    // because that lets us take a faster branch in the code. 0.69 is chosen because 0.69 + log10(2) is
    // less than one by a reasonable epsilon that will account for any floating point error.
    //
    // We want to set digitExponent to floor(log10(v)) + 1
    //  v = mantissa*2^exponent
    //  log2(v) = log2(mantissa) + exponent;
    //  log10(v) = log2(v) * log10(2)
    //  floor(log2(v)) = mantissaHighBitIdx + exponent;
    //  log10(v) - log10(2) < (mantissaHighBitIdx + exponent) * log10(2) <= log10(v)
    //  log10(v) < (mantissaHighBitIdx + exponent) * log10(2) + log10(2) <= log10(v) + log10(2)
    //  floor( log10(v) ) < ceil( (mantissaHighBitIdx + exponent) * log10(2) ) <= floor( log10(v) ) + 1
    const double log10_2 = 0.30102999566398119521373889472449;
    int32_t digitExponent = (int32_t)(ceil(double((int32_t)mantissaHighBitIdx + exponent) * log10_2 - 0.69));

    // if the digit exponent is smaller than the smallest desired digit for fractional cutoff,
    // pull the digit back into legal range at which point we will round to the appropriate value.
    // Note that while our value for digitExponent is still an estimate, this is safe because it
    // only increases the number. This will either correct digitExponent to an accurate value or it
    // will clamp it above the accurate value.
    if (cutoffMode == CutoffMode_FractionLength && digitExponent <= -(int32_t)cutoffNumber)
    {
        digitExponent = -(int32_t)cutoffNumber + 1;
    }

    // Divide value by 10^digitExponent.
    if (digitExponent > 0)
    {
        // The exponent is positive creating a division so we multiply up the scale.
        BigInt temp;
        BigInt_MultiplyPow10(&temp, scale, digitExponent);
        scale = temp;
    }
    else if (digitExponent < 0)
    {
        // The exponent is negative creating a multiplication so we multiply up the scaledValue,
        // scaledMarginLow and scaledMarginHigh.
        BigInt pow10;
        BigInt_Pow10(&pow10, -digitExponent);

        BigInt temp;
        BigInt_Multiply(&temp, scaledValue, pow10);
        scaledValue = temp;

        BigInt_Multiply(&temp, scaledMarginLow, pow10);
        scaledMarginLow = temp;

        if (pScaledMarginHigh != &scaledMarginLow)
            BigInt_Multiply2(pScaledMarginHigh, scaledMarginLow);
    }

    // If (value >= 1), our estimate for digitExponent was too low
    if (BigInt_Compare(scaledValue, scale) >= 0)
    {
        // The exponent estimate was incorrect.
        // Increment the exponent and don't perform the premultiply needed
        // for the first loop iteration.
        digitExponent = digitExponent + 1;
    }
    else
    {
        // The exponent estimate was correct.
        // Multiply larger by the output base to prepare for the first loop iteration.
        BigInt_Multiply10(&scaledValue);
        BigInt_Multiply10(&scaledMarginLow);
        if (pScaledMarginHigh != &scaledMarginLow)
            BigInt_Multiply2(pScaledMarginHigh, scaledMarginLow);
    }

    // Compute the cutoff exponent (the exponent of the final digit to print).
    // Default to the maximum size of the output buffer.
    int32_t cutoffExponent = digitExponent - bufferSize;
    switch (cutoffMode)
    {
    // print digits until we pass the accuracy margin limits or buffer size
    case CutoffMode_Unique:
        break;

    // print cutoffNumber of digits or until we reach the buffer size
    case CutoffMode_TotalLength:
    {
        int32_t desiredCutoffExponent = digitExponent - (int32_t)cutoffNumber;
        if (desiredCutoffExponent > cutoffExponent)
            cutoffExponent = desiredCutoffExponent;
    }
    break;

    // print cutoffNumber digits past the decimal point or until we reach the buffer size
    case CutoffMode_FractionLength:
    {
        int32_t desiredCutoffExponent = -(int32_t)cutoffNumber;
        if (desiredCutoffExponent > cutoffExponent)
            cutoffExponent = desiredCutoffExponent;
    }
    break;
    }

    // Output the exponent of the first digit we will print
    *pOutExponent = digitExponent - 1;

    // In preparation for calling BigInt_DivideWithRemainder_MaxQuotient9(),
    // we need to scale up our values such that the highest block of the denominator
    // is greater than or equal to 8. We also need to guarantee that the numerator
    // can never have a length greater than the denominator after each loop iteration.
    // This requires the highest block of the denominator to be less than or equal to
    // 429496729 which is the highest number that can be multiplied by 10 without
    // overflowing to a new block.
    assert(scale.GetLength() > 0);
    uint32_t hiBlock = scale.Geboollock(scale.GetLength() - 1);
    if (hiBlock < 8 || hiBlock > 429496729)
    {
        // Perform a bit shift on all values to get the highest block of the denominator into
        // the range [8,429496729]. We are more likely to make accurate quotient estimations
        // in BigInt_DivideWithRemainder_MaxQuotient9() with higher denominator values so
        // we shift the denominator to place the highest bit at index 27 of the highest block.
        // This is safe because (2^28 - 1) = 268435455 which is less than 429496729. This means
        // that all values with a highest bit at index 27 are within range.
        uint32_t hiBlockLog2 = log2i(hiBlock);
        assert(hiBlockLog2 < 3 || hiBlockLog2 > 27);
        uint32_t shift = (32 + 27 - hiBlockLog2) % 32;

        BigInt_ShiftLeft(&scale, shift);
        BigInt_ShiftLeft(&scaledValue, shift);
        BigInt_ShiftLeft(&scaledMarginLow, shift);
        if (pScaledMarginHigh != &scaledMarginLow)
            BigInt_Multiply2(pScaledMarginHigh, scaledMarginLow);
    }

    // These values are used to inspect why the print loop terminated so we can properly
    // round the final digit.
    bool low;             // did the value get within marginLow distance from zero
    bool high;            // did the value get within marginHigh distance from one
    uint32_t outputDigit; // current digit being output

    if (cutoffMode == CutoffMode_Unique)
    {
        // For the unique cutoff mode, we will try to print until we have reached a level of
        // precision that uniquely distinguishes this value from its neighbors. If we run
        // out of space in the output buffer, we terminate early.
        for (;;)
        {
            digitExponent = digitExponent - 1;

            // divide out the scale to extract the digit
            outputDigit = BigInt_DivideWithRemainder_MaxQuotient9(&scaledValue, scale);
            assert(outputDigit < 10);

            // update the high end of the value
            BigInt scaledValueHigh;
            BigInt_Add(&scaledValueHigh, scaledValue, *pScaledMarginHigh);

            // stop looping if we are far enough away from our neighboring values
            // or if we have reached the cutoff digit
            low = BigInt_Compare(scaledValue, scaledMarginLow) < 0;
            high = BigInt_Compare(scaledValueHigh, scale) > 0;
            if (low | high | (digitExponent == cutoffExponent))
                break;

            // store the output digit
            *pCurDigit = (char)('0' + outputDigit);
            ++pCurDigit;

            // multiply larger by the output base
            BigInt_Multiply10(&scaledValue);
            BigInt_Multiply10(&scaledMarginLow);
            if (pScaledMarginHigh != &scaledMarginLow)
                BigInt_Multiply2(pScaledMarginHigh, scaledMarginLow);
        }
    }
    else
    {
        // For length based cutoff modes, we will try to print until we
        // have exhausted all precision (i.e. all remaining digits are zeros) or
        // until we reach the desired cutoff digit.
        low = false;
        high = false;

        for (;;)
        {
            digitExponent = digitExponent - 1;

            // divide out the scale to extract the digit
            outputDigit = BigInt_DivideWithRemainder_MaxQuotient9(&scaledValue, scale);
            assert(outputDigit < 10);

            if (scaledValue.IsZero() | (digitExponent == cutoffExponent))
                break;

            // store the output digit
            *pCurDigit = (char)('0' + outputDigit);
            ++pCurDigit;

            // multiply larger by the output base
            BigInt_Multiply10(&scaledValue);
        }
    }

    // round off the final digit
    // default to rounding down if value got too close to 0
    bool roundDown = low;

    // if it is legal to round up and down
    if (low == high)
    {
        // round to the closest digit by comparing value with 0.5. To do this we need to convert
        // the inequality to large integer values.
        //  compare( value, 0.5 )
        //  compare( scale * value, scale * 0.5 )
        //  compare( 2 * scale * value, scale )
        BigInt_Multiply2(&scaledValue);
        int32_t compare = BigInt_Compare(scaledValue, scale);
        roundDown = compare < 0;

        // if we are directly in the middle, round towards the even digit (i.e. IEEE rouding rules)
        if (compare == 0)
            roundDown = (outputDigit & 1) == 0;
    }

    // print the rounded digit
    if (roundDown)
    {
        *pCurDigit = (char)('0' + outputDigit);
        ++pCurDigit;
    }
    else
    {
        // handle rounding up
        if (outputDigit == 9)
        {
            // find the first non-nine prior digit
            for (;;)
            {
                // if we are at the first digit
                if (pCurDigit == pOubooluffer)
                {
                    // output 1 at the next highest exponent
                    *pCurDigit = '1';
                    ++pCurDigit;
                    *pOutExponent += 1;
                    break;
                }

                --pCurDigit;
                if (*pCurDigit != '9')
                {
                    // increment the digit
                    *pCurDigit += 1;
                    ++pCurDigit;
                    break;
                }
            }
        }
        else
        {
            // values in the range [0,8] can perform a simple round up
            *pCurDigit = (char)('0' + outputDigit + 1);
            ++pCurDigit;
        }
    }

    // return the number of digits output
    uint32_t outputLen = (uint32_t)(pCurDigit - pOubooluffer);
    assert(outputLen <= bufferSize);
    return outputLen;
}

Here is the call graph for this function:

Here is the caller graph for this function:

Variable Documentation

c_BigInt_MaxBlocks

const uint32_t c_BigInt_MaxBlocks = 35

Definition at line 59 of file bigint.h.