mathr.h File Reference

Real numbers math library. More...

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Macros
#define	PI   3.1415926535897932384626433832795028841971693994
#define	EULERS   2.7182818284590452353602874713526624977572470937
#define	INFP   0x7FF0000000000000ull
#define	INFN   0xFFF0000000000000ull
#define	NAN   0x7FFFFFFFFFFFFFFFull
#define	sgn(x)   (x > 0 ? 1 : x < 0 ? -1 : 0)
#define	abs(x)   (x > 0 ? x : -x)

Functions
double	fabs (double x)
	Returns the absolute value of x. More...
double	ceil (double x)
	Ceiling function. More...
double	floor (double x)
	Floor function. More...
double	round (double x)
	Round function. More...
double	trunc (double x)
	Truncate function. More...
double	exp (double x)
	Returns the exponential of x. More...
double	sqrt (double x)
	Square root function. More...
double	cbrt (double x)
	Cube root function. More...
double	log (double x)
	Natural logarithm function (base e) More...
double	log10 (double x)
	Base 10 logarithm function. More...
double	cos (double x)
	Cosine function. More...
double	sin (double x)
	Sine function. More...
double	tan (double x)
	Tangent function. More...
double	sec (double x)
	Secant function. More...
double	csc (double x)
	Cosecant function. More...
double	cot (double x)
	Cotangent function. More...
double	exs (double x)
	Exsecant function. More...
double	exc (double x)
	Excosecant function. More...
double	crd (double x)
	Chord function. More...
double	acos (double x)
	Inverse cosine function. More...
double	asin (double x)
	Inverse sine function. More...
double	atan (double x)
	Inverse tangent function. More...
double	asec (double x)
	Inverse secant function. More...
double	acsc (double x)
	Inverse cosecant function. More...
double	acot (double x)
	Inverse cotangent function. More...
double	aexs (double x)
	Inverse exsecant function. More...
double	aexc (double x)
	Inverse excosecant function. More...
double	acrd (double x)
	Inverse chord function. More...
double	cosh (double x)
	Hyperbolic cosine function. More...
double	sinh (double x)
	Hyperbolic sine function. More...
double	tanh (double x)
	Hyperbolic tangent function. More...
double	sech (double x)
	Hyperbolic secant function. More...
double	csch (double x)
	Hyperbolic cosecant function. More...
double	coth (double x)
	Hyperbolic cotangent function. More...
double	acosh (double x)
	Inverse hyperbolic cosine function. More...
double	asinh (double x)
	Inverse hyperbolic sine function. More...
double	atanh (double x)
	Inverse hyperbolic tangent function. More...
double	asech (double x)
	Inverse hyperbolic secant function. More...
double	acsch (double x)
	Inverse hyperbolic cosecant function. More...
double	acoth (double x)
	Inverse hyperbolic cotangent function. More...
double	ver (double x)
	Versed sine function. More...
double	vcs (double x)
	Versed cosine function. More...
double	cvs (double x)
	Coversed sine function. More...
double	cvc (double x)
	Coversed cosine function. More...
double	hv (double x)
	Haversed sine function. More...
double	hvc (double x)
	Haversed cosine function. More...
double	hcv (double x)
	Hacoversed sine function. More...
double	hcc (double x)
	Hacoversed cosine function. More...
double	aver (double x)
	Inverse versed sine function. More...
double	avcs (double x)
	Inverse versed sine. More...
double	acvs (double x)
	Inverse coversed sine function. More...
double	acvc (double x)
	Inverse versed cosine. More...
double	ahv (double x)
	Inverse haversed sine. More...
double	ahvc (double x)
	Inverse haversed cosine. More...
double	ahcv (double x)
	Inverse hacoversed sine. More...
double	ahcc (double x)
	Inverse hacoversed cosine. More...
double	pow (double x, double y)
	Expontation function. More...
double	fmod (double x, double y)
	Return x mod y in exact arithmetic. More...
double	atan2 (double y, double x)
	Inverse tangent function. More...
double	hypot (double x, double y)
	hypot More...
double	log2p (double x, double y)
double	log1p (double x)
double	expm1 (double x)
double	scalbn (double x, int n)
double	copysign (double x, double y)
	Returns a value with the magnitude of x and with the sign bit of y. More...
int	rempio2 (double x, double *y)
unsigned int	log2i (unsigned int x)

Detailed Description

Real numbers math library.

The library is based on fdlib by Sun Microsystems.

The original library can be downloaded at netlib.org:
http://www.netlib.org/fdlibm/

or from mirror site hensa.ac.uk:
http://www.hensa.ac.uk/

More info on double precision floating point at Wikipedia:
https://wikipedia.org/wiki/Double-precision_floating-point_format

Author

Carsten Sonne Larsen <cs@in.nosp@m.nola.nosp@m.n.net>

Definition in file mathr.h.

Macro Definition Documentation

abs

#define abs

(

x

)

(x > 0 ? x : -x)

Definition at line 55 of file mathr.h.

EULERS

#define EULERS   2.7182818284590452353602874713526624977572470937

Definition at line 50 of file mathr.h.

INFN

#define INFN   0xFFF0000000000000ull

Definition at line 52 of file mathr.h.

INFP

#define INFP   0x7FF0000000000000ull

Definition at line 51 of file mathr.h.

NAN

#define NAN   0x7FFFFFFFFFFFFFFFull

Definition at line 53 of file mathr.h.

PI

#define PI   3.1415926535897932384626433832795028841971693994

Definition at line 49 of file mathr.h.

sgn

#define sgn

(

x

)

(x > 0 ? 1 : x < 0 ? -1 : 0)

Definition at line 54 of file mathr.h.

Function Documentation

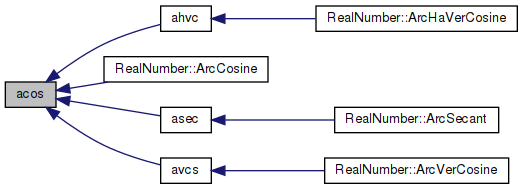
acos()

double acos

(

double

x

)

Inverse cosine function.

Method
    acos(x)  = pi/2 - asin(x)
    acos(-x) = pi/2 + asin(x)

    For |x|<=0.5
    acos(x)  = pi/2 - (x + x*x^2*R(x^2))        (see asin.c)

    For x>0.5
    acos(x)  = pi/2 - (pi/2 - 2asin(sqrt((1-x)/2)))
             = 2asin(sqrt((1-x)/2))
             = 2s + 2s*z*R(z)   ...z=(1-x)/2, s=sqrt(z)
             = 2f + (2c + 2s*z*R(z))
    where f=hi part of s, and c = (z-f*f)/(s+f) is the correction term
    for f so that f+c ~ sqrt(z).

    For x<-0.5
    acos(x)  = pi - 2asin(sqrt((1-|x|)/2))
             = pi - 0.5*(s+s*z*R(z)), where z=(1-|x|)/2,s=sqrt(z)

Special cases
    if x is NaN, return NaN
    if |x|>1, return NaN

Definition at line 92 of file acos.c.

References one, pi, pio2_hi, pio2_lo, pS0, pS1, pS2, pS3, pS4, pS5, qS1, qS2, qS3, qS4, and sqrt().

Referenced by ahvc(), RealNumber::ArcCosine(), asec(), and avcs().

{
    double z, p, q, r, w, s, c, df;
    int32_t hx, ix;
    uint32_t lx;

    GET_HIGH_WORD(hx, x);
    ix = hx & 0x7FFFFFFF;

    // |x| >= 1
    if (ix >= 0x3FF00000)
    {
        GET_LOW_WORD(lx, x);

        // |x|==1
        if (((ix - 0x3FF00000) | lx) == 0)
        {
            if (hx > 0)
            {
                // acos(1) = 0
                return 0.0;
            }

            // acos(-1) = pi
            return pi + 2.0 * pio2_lo;
        }

        // acos(|x|>1) is NaN
        return NAN;
    }

    // |x| < 0.5
    if (ix < 0x3FE00000)
    {
        // if |x|<2**-57
        if (ix <= 0x3C600000)
        {
            return pio2_hi + pio2_lo;
        }
        z = x * x;
        p = z * (pS0 + z * (pS1 + z * (pS2 + z * (pS3 + z * (pS4 + z * pS5)))));
        q = one + z * (qS1 + z * (qS2 + z * (qS3 + z * qS4)));
        r = p / q;
        return pio2_hi - (x - (pio2_lo - x * r));
    }

    // x < -0.5
    if (hx < 0)
    {
        z = (one + x) * 0.5;
        p = z * (pS0 + z * (pS1 + z * (pS2 + z * (pS3 + z * (pS4 + z * pS5)))));
        q = one + z * (qS1 + z * (qS2 + z * (qS3 + z * qS4)));
        s = sqrt(z);
        r = p / q;
        w = r * s - pio2_lo;
        return pi - 2.0 * (s + w);
    }

    // x > 0.5
    z = (one - x) * 0.5;
    s = sqrt(z);
    df = s;
    SET_LOW_WORD(df, 0);
    c = (z - df * df) / (s + df);
    p = z * (pS0 + z * (pS1 + z * (pS2 + z * (pS3 + z * (pS4 + z * pS5)))));
    q = one + z * (qS1 + z * (qS2 + z * (qS3 + z * qS4)));
    r = p / q;
    w = r * s + c;
    return 2.0 * (df + w);
}

Here is the call graph for this function:

Here is the caller graph for this function:

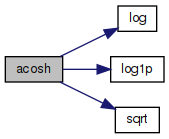
acosh()

double acosh

(

double

x

)

Inverse hyperbolic cosine function.

Based on
    acosh(x) = log [ x + sqrt(x*x-1) ]

we have
    acosh(x) = log(x)+ln2, if x is large; else
    acosh(x) = log(2x-1/(sqrt(x*x-1)+x)) if x>2; else
    acosh(x) = log1p(t+sqrt(2.0*t+t*t)); where t=x-1

Special cases
    acosh(x) is NaN if x<1
    acosh(NaN) is NaN

Definition at line 69 of file acosh.c.

References ln2, log(), log1p(), one, and sqrt().

Referenced by RealNumber::HypArcCosine().

{
    double t;
    int32_t hx, lx;

    GET_HIGH_WORD(hx, x);
    GET_LOW_WORD(lx, x);

    // x < 1
    if (hx < 0x3FF00000)
    {
        return NAN;
    }

    // x > 2**28
    if (hx >= 0x41B00000)
    {
        // x is inf or NaN
        if (hx >= 0x7FF00000)
        {
            return NAN;
        }

        // acosh(huge) = log(2x)
        return log(x) + ln2;
    }

    // acosh(1) = 0
    if (((hx - 0x3FF00000) | lx) == 0)
    {
        return 0.0;
    }

    // 2**28 > x > 2
    if (hx > 0x40000000)
    {
        t = x * x;
        return log(2.0 * x - one / (x + sqrt(t - one)));
    }

    // 1 < x < 2
    t = x - one;
    return log1p(t + sqrt(2.0 * t + t * t));
}

Here is the call graph for this function:

Here is the caller graph for this function:

acot()

double acot

(

double

x

)

Inverse cotangent function.

Method
    arccot(x) = arctan(1/x)

Definition at line 45 of file acot.c.

References atan().

Referenced by RealNumber::ArcCotangent().

{
    double a = 1.0 / x;
    double b = atan(a);
    return b;
}

Here is the call graph for this function:

Here is the caller graph for this function:

acoth()

double acoth

(

double

x

)

Inverse hyperbolic cotangent function.

Method
                          x + 1
    acoth(x) = 0.5 * ln( ----— )
                          x - 1
    when x in [-1, 1]
    acoth(x) = NaN

Definition at line 49 of file acoth.c.

References log().

Referenced by RealNumber::HypArcCotangent().

{
    double a, b, c, d;

    if (x <= 1 && x >= -1)
    {
        return NAN;
    }

    a = x + 1.0;
    b = x - 1.0;
    c = a / b;
    d = 0.5 * log(c);
    return d;
}

Here is the call graph for this function:

Here is the caller graph for this function:

acrd()

double acrd

(

double

x

)

Inverse chord function.

Method
    arccrd(x) = 2*arcsin(x/2)

Definition at line 45 of file acrd.c.

References asin().

Referenced by RealNumber::ArcChord().

{
    double a = x / 2.0;
    double b = asin(a);
    double c = 2.0 * b;
    return c;
}

Here is the call graph for this function:

Here is the caller graph for this function:

acsc()

double acsc

(

double

x

)

Inverse cosecant function.

Method
    arccsc(x) = arcsin(1/x)

Definition at line 45 of file acsc.c.

References asin().

Referenced by RealNumber::ArcCosecant().

{
    double a = 1.0 / x;
    double b = asin(a);
    return b;
}

Here is the call graph for this function:

Here is the caller graph for this function:

acsch()

double acsch

(

double

x

)

Inverse hyperbolic cosecant function.

Method
                    1+sqrt(1+x*x)
    acsch(x) = ln( ------------— )
                          x
    when x is 0
    acsch(x) = NaN

Definition at line 49 of file acsch.c.

References log(), and sqrt().

Referenced by RealNumber::HypArcCosecant().

{
    double a, b, c, d, e, f;

    if (TRIG_INEXACT(x))
    {
        return NAN;
    }

    a = x * x;
    b = a + 1.0;
    c = sqrt(b);
    d = 1.0 + c;
    e = d / x;
    f = log(e);
    return f;
}

Here is the call graph for this function:

Here is the caller graph for this function:

acvc()

double acvc

(

double

x

)

Inverse versed cosine.

Method
    acvc(x) = asin(1+x)

Definition at line 45 of file acvc.c.

References asin().

Referenced by RealNumber::ArcCoVerCosine().

{
    return asin(1.0 + x);
}

Here is the call graph for this function:

Here is the caller graph for this function:

acvs()

double acvs

(

double

x

)

Inverse coversed sine function.

Definition at line 40 of file acvs.c.

References atan(), and sqrt().

Referenced by RealNumber::ArcCoVerSine().

{
    double a = 1.0 - x;
    double b = 2.0 * x - x * x;
    double c = sqrt(b);
    double d = atan(a / c);  
    return d;
}

Here is the call graph for this function:

Here is the caller graph for this function:

aexc()

double aexc

(

double

x

)

Inverse excosecant function.

Method
    aexcsc(x) = arccsc(x+1)
              = arcsin(1/(x+1))

Definition at line 46 of file aexc.c.

References asin().

Referenced by RealNumber::ArcExCosecant().

{
    double a, b, c;

    if (x > -2.0 && x < 0.0)
        return NAN;

    a = x + 1;
    b = 1 / a;
    c = asin(b);
    return c;
}

Here is the call graph for this function:

Here is the caller graph for this function:

aexs()

double aexs

(

double

x

)

Inverse exsecant function.

Method
    aexsec(x) = arcsec(x+1)
              = arccos(1/(x+1))
              = arctan(sqrt(x^2+2*X))

Definition at line 47 of file aexs.c.

References atan(), and sqrt().

Referenced by RealNumber::ArcExSecant().

{
    double a, b, c;

    if (x > -2.0 && x < 0.0)
        return NAN;

    a = x * x + 2 * x;
    b = sqrt(a);
    c = atan(b);
    return c;
}

Here is the call graph for this function:

Here is the caller graph for this function:

ahcc()

double ahcc

(

double

x

)

Inverse hacoversed cosine.

Definition at line 40 of file ahcc.c.

Referenced by RealNumber::ArcHaCoVerCosine().

{
    // TODO: Implement ahcc(double)
    return NAN;
}

Here is the caller graph for this function:

ahcv()

double ahcv

(

double

x

)

Inverse hacoversed sine.

Definition at line 40 of file ahcv.c.

Referenced by RealNumber::ArcHaCoVerSine().

{
    // TODO: Implement ahcv(double)
    return NAN;
}

Here is the caller graph for this function:

ahv()

double ahv

(

double

x

)

Inverse haversed sine.

Definition at line 40 of file ahv.c.

References atan(), and sqrt().

Referenced by RealNumber::ArcHaVerSine().

{
    double a = x - x * x;
    double b = 2.0 * sqrt(a);
    double c = 1.0 - 2.0 * x;
    double d = atan(b / c);   
    return d;
}

Here is the call graph for this function:

Here is the caller graph for this function:

ahvc()

double ahvc

(

double

x

)

Inverse haversed cosine.

Definition at line 40 of file ahvc.c.

References acos(), and sqrt().

Referenced by RealNumber::ArcHaVerCosine().

{
    double a = sqrt(x);
    double b = acos(a);
    double c = 2.0 * b;    
    return c;
}

Here is the call graph for this function:

Here is the caller graph for this function:

asec()

double asec

(

double

x

)

Inverse secant function.

Method
    arcsec(x) = arccos(1/x)

Definition at line 45 of file asec.c.

References acos().

Referenced by RealNumber::ArcSecant().

{
    double a = 1.0 / x;
    double b = acos(a);
    return b;
}

Here is the call graph for this function:

Here is the caller graph for this function:

asech()

double asech

(

double

x

)

Inverse hyperbolic secant function.

Method
                    1+sqrt(1-x*x)
    asech(x) = ln( ------------— )
                          x
    when x <= 0
    asech(x) = NaN

    when x > 1
    asech(x) = NaN

Definition at line 52 of file asech.c.

References log(), and sqrt().

Referenced by RealNumber::HypArcSecant().

{
    double a, b, c, d, e, f;

    if (TRIG_INEXACT(x) || x < 0.0 || x > 1.0)
    {
        return NAN;
    }

    a = x * x;
    b = 1.0 - a;
    c = sqrt(b);
    d = 1.0 + c;
    e = d / x;
    f = log(e);
    return f;
}

Here is the call graph for this function:

Here is the caller graph for this function:

asin()

double asin

(

double

x

)

Inverse sine function.

Method

Since  asin(x) = x + x^3/6 + x^5*3/40 + x^7*15/336 + ...
we approximate asin(x) on [0,0.5] by
     asin(x) = x + x*x^2*R(x^2)
where
     R(x^2) is a rational approximation of (asin(x)-x)/x^3
and its remez error is bounded by
     |(asin(x)-x)/x^3 - R(x^2)| < 2^(-58.75)

For x in [0.5,1]
     asin(x) = pi/2-2*asin(sqrt((1-x)/2))
Let y = (1-x), z = y/2, s := sqrt(z), and pio2_hi+pio2_lo=pi/2;
then for x>0.98
     asin(x) = pi/2 - 2*(s+s*z*R(z))
             = pio2_hi - (2*(s+s*z*R(z)) - pio2_lo)

For x<=0.98, let pio4_hi = pio2_hi/2, then
     f = hi part of s;
     c = sqrt(z) - f = (z-f*f)/(s+f)     ...f+c=sqrt(z)
and
     asin(x) = pi/2 - 2*(s+s*z*R(z))
             = pio4_hi+(pio4-2s)-(2s*z*R(z)-pio2_lo)
             = pio4_hi+(pio4-2f)-(2s*z*R(z)-(pio2_lo+2c))

Special cases
    if x is NaN, return NaN
    if |x|>1, return NaN

Definition at line 100 of file asin.c.

References fabs(), huge, one, pio2_hi, pio2_lo, pio4_hi, pS0, pS1, pS2, pS3, pS4, pS5, qS1, qS2, qS3, qS4, and sqrt().

Referenced by acrd(), acsc(), acvc(), aexc(), and RealNumber::ArcSine().

{
    double t, w, p, q, c, r, s;
    int32_t hx, ix;
    GET_HIGH_WORD(hx, x);
    ix = hx & 0x7fffffff;
    if (ix >= 0x3ff00000)
    { /* |x|>= 1 */
        uint32_t lx;
        GET_LOW_WORD(lx, x);
        if (((ix - 0x3ff00000) | lx) == 0)
            /* asin(1)=+-pi/2 with inexact */
            return x * pio2_hi + x * pio2_lo;
        return NAN; /* asin(|x|>1) is NaN */
    }
    else if (ix < 0x3fe00000)
    { /* |x|<0.5 */
        if (ix < 0x3e400000)
        { /* if |x| < 2**-27 */
            if (huge + x > one)
            {
                return x; /* return x with inexact if x!=0*/
            }
            else
            {
                t = 0;
            }
        }
        else
        {
            t = x * x;
        }

        p = t * (pS0 + t * (pS1 + t * (pS2 + t * (pS3 + t * (pS4 + t * pS5)))));
        q = one + t * (qS1 + t * (qS2 + t * (qS3 + t * qS4)));
        w = p / q;
        return x + x * w;
    }
    /* 1> |x|>= 0.5 */
    w = one - fabs(x);
    t = w * 0.5;
    p = t * (pS0 + t * (pS1 + t * (pS2 + t * (pS3 + t * (pS4 + t * pS5)))));
    q = one + t * (qS1 + t * (qS2 + t * (qS3 + t * qS4)));
    s = sqrt(t);
    if (ix >= 0x3FEF3333)
    { /* if |x| > 0.975 */
        w = p / q;
        t = pio2_hi - (2.0 * (s + s * w) - pio2_lo);
    }
    else
    {
        w = s;
        SET_LOW_WORD(w, 0);
        c = (t - w * w) / (s + w);
        r = p / q;
        p = 2.0 * s * r - (pio2_lo - 2.0 * c);
        q = pio4_hi - 2.0 * w;
        t = pio4_hi - (p - q);
    }
    if (hx > 0)
        return t;
    else
        return -t;
}

Here is the call graph for this function:

Here is the caller graph for this function:

asinh()

double asinh

(

double

x

)

Inverse hyperbolic sine function.

Method
    Based on
    asinh(x) = sign(x) * log [ |x| + sqrt(x*x+1) ]

    we have
    asinh(x) = x  if  1+x*x=1,
             = sign(x)*(log(x)+ln2)) for large |x|, else
             = sign(x)*log(2|x|+1/(|x|+sqrt(x*x+1))) if|x|>2, else
             = sign(x)*log1p(|x| + x^2/(1 + sqrt(1+x^2)))

Definition at line 68 of file asinh.c.

References fabs(), huge, ln2, log(), log1p(), one, and sqrt().

Referenced by RealNumber::HypArcSine().

{
    double t, w;
    int32_t hx, ix;
    GET_HIGH_WORD(hx, x);
    ix = hx & 0x7fffffff;
    if (ix >= 0x7ff00000)
        return x + x; /* x is inf or NaN */
    if (ix < 0x3e300000)
    { /* |x|<2**-28 */
        if (huge + x > one)
            return x; /* return x inexact except 0 */
    }
    if (ix > 0x41b00000)
    { /* |x| > 2**28 */
        w = log(fabs(x)) + ln2;
    }
    else if (ix > 0x40000000)
    { /* 2**28 > |x| > 2.0 */
        t = fabs(x);
        w = log(2.0 * t + one / (sqrt(x * x + one) + t));
    }
    else
    { /* 2.0 > |x| > 2**-28 */
        t = x * x;
        w = log1p(fabs(x) + t / (one + sqrt(one + t)));
    }
    if (hx > 0)
        return w;
    else
        return -w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

atan()

double atan

(

double

x

)

Inverse tangent function.

Method
    1. Reduce x to positive by atan(x) = -atan(-x).
    2. According to the integer k=4t+0.25 chopped, t=x, the argument
       is further reduced to one of the following intervals and the
       arctangent of t is evaluated by the corresponding formula:

    [0,7/16]      atan(x) = t-t^3*(a1+t^2*(a2+...(a10+t^2*a11)...)
    [7/16,11/16]  atan(x) = atan(1/2) + atan( (t-0.5)/(1+t/2) )
    [11/16.19/16] atan(x) = atan( 1 ) + atan( (t-1)/(1+t) )
    [19/16,39/16] atan(x) = atan(3/2) + atan( (t-1.5)/(1+1.5t) )
    [39/16,INF]   atan(x) = atan(INF) + atan( -1/t )

Constants
    The hexadecimal values are the intended ones for the following
    constants. The decimal values may be used, provided that the
    compiler will convert from decimal to binary accurately enough
    to produce the hexadecimal values shown.

Definition at line 103 of file atan.c.

References aT, atanhi, atanlo, fabs(), huge, and one.

Referenced by acot(), acvs(), aexs(), ahv(), RealNumber::ArcTangent(), atan2(), and aver().

{
    double w, s1, s2, z;
    int32_t ix, hx, id;

    GET_HIGH_WORD(hx, x);
    ix = hx & 0x7fffffff;
    if (ix >= 0x44100000)
    { /* if |x| >= 2^66 */
        uint32_t low;

        GET_LOW_WORD(low, x);
        if (ix > 0x7ff00000 || (ix == 0x7ff00000 && (low != 0)))
            return NAN;
        if (hx > 0)
            return atanhi[3] + atanlo[3];
        else
            return -atanhi[3] - atanlo[3];
    }
    if (ix < 0x3fdc0000)
    { /* |x| < 0.4375 */
        if (ix < 0x3e200000)
        { /* |x| < 2^-29 */
            if (huge + x > one)
                return x; /* raise inexact */
        }
        id = -1;
    }
    else
    {
        x = fabs(x);
        if (ix < 0x3ff30000)
        { /* |x| < 1.1875 */
            if (ix < 0x3fe60000)
            { /* 7/16 <=|x|<11/16 */
                id = 0;
                x = (2.0 * x - one) / (2.0 + x);
            }
            else
            { /* 11/16<=|x|< 19/16 */
                id = 1;
                x = (x - one) / (x + one);
            }
        }
        else
        {
            if (ix < 0x40038000)
            { /* |x| < 2.4375 */
                id = 2;
                x = (x - 1.5) / (one + 1.5 * x);
            }
            else
            { /* 2.4375 <= |x| < 2^66 */
                id = 3;
                x = -1.0 / x;
            }
        }
    }
    /* end of argument reduction */
    z = x * x;
    w = z * z;
    /* break sum from i=0 to 10 aT[i]z**(i+1) into odd and even poly */
    s1 = z * (aT[0] + w * (aT[2] + w * (aT[4] + w * (aT[6] + w * (aT[8] + w * aT[10])))));
    s2 = w * (aT[1] + w * (aT[3] + w * (aT[5] + w * (aT[7] + w * aT[9]))));
    if (id < 0)
    {
        return x - x * (s1 + s2);
    }

    z = atanhi[id] - ((x * (s1 + s2) - atanlo[id]) - x);
    return (hx < 0) ? -z : z;
}

Here is the call graph for this function:

Here is the caller graph for this function:

atan2()

double atan2	(	double	y,
		double	x
	)

Inverse tangent function.

Parameters

y,x

Method
    1. Reduce y to positive by atan2(y,x)=-atan2(-y,x).
    2. Reduce x to positive by (if x and y are unexceptional):
       ARG (x+iy) = arctan(y/x)           ... if x > 0,
       ARG (x+iy) = pi - arctan[y/(-x)]   ... if x < 0,

Special cases
    ATAN2((anything), NaN ) is NaN;
    ATAN2(NAN , (anything) ) is NaN;
    ATAN2(+-0, +(anything but NaN)) is +-0  ;
    ATAN2(+-0, -(anything but NaN)) is +-pi ;
    ATAN2(+-(anything but 0 and NaN), 0) is +-pi/2;
    ATAN2(+-(anything but INF and NaN), +INF) is +-0 ;
    ATAN2(+-(anything but INF and NaN), -INF) is +-pi;
    ATAN2(+-INF,+INF ) is +-pi/4 ;
    ATAN2(+-INF,-INF ) is +-3pi/4;
    ATAN2(+-INF, (anything but,0,NaN, and INF)) is +-pi/2;

Constants
    The hexadecimal values are the intended ones for the following
    constants. The decimal values may be used, provided that the
    compiler will convert from decimal to binary accurately enough
    to produce the hexadecimal values shown.

Definition at line 87 of file atan2.c.

References atan(), fabs(), pi, pi_lo, pi_o_2, pi_o_4, tiny, and zero.

Referenced by clog(), and cpow().

{
    double z;
    int32_t k, m, hx, hy, ix, iy;
    uint32_t lx, ly;

    EXTRACT_WORDS(hx, lx, x);
    ix = hx & 0x7fffffff;
    EXTRACT_WORDS(hy, ly, y);
    iy = hy & 0x7fffffff;
    if (((ix | ((lx | -lx) >> 31)) > 0x7ff00000) ||
        ((iy | ((ly | -ly) >> 31)) > 0x7ff00000)) /* x or y is NaN */
        return x + y;
    if (((hx - 0x3ff00000) | lx) == 0)
        return atan(y);                      /* x=1.0 */
    m = ((hy >> 31) & 1) | ((hx >> 30) & 2); /* 2*sign(x)+sign(y) */

    /* when y = 0 */
    if ((iy | ly) == 0)
    {
        switch (m)
        {
        case 0:
        case 1:
            return y; /* atan(+-0,+anything)=+-0 */
        case 2:
            return pi + tiny; /* atan(+0,-anything) = pi */
        case 3:
            return -pi - tiny; /* atan(-0,-anything) =-pi */
        }
    }
    /* when x = 0 */
    if ((ix | lx) == 0)
        return (hy < 0) ? -pi_o_2 - tiny : pi_o_2 + tiny;

    /* when x is INF */
    if (ix == 0x7ff00000)
    {
        if (iy == 0x7ff00000)
        {
            switch (m)
            {
            case 0:
                return pi_o_4 + tiny; /* atan(+INF,+INF) */
            case 1:
                return -pi_o_4 - tiny; /* atan(-INF,+INF) */
            case 2:
                return 3.0 * pi_o_4 + tiny; /*atan(+INF,-INF)*/
            case 3:
                return -3.0 * pi_o_4 - tiny; /*atan(-INF,-INF)*/
            }
        }
        else
        {
            switch (m)
            {
            case 0:
                return zero; /* atan(+...,+INF) */
            case 1:
                return -zero; /* atan(-...,+INF) */
            case 2:
                return pi + tiny; /* atan(+...,-INF) */
            case 3:
                return -pi - tiny; /* atan(-...,-INF) */
            }
        }
    }
    /* when y is INF */
    if (iy == 0x7ff00000)
        return (hy < 0) ? -pi_o_2 - tiny : pi_o_2 + tiny;

    /* compute y/x */
    k = (iy - ix) >> 20;
    if (k > 60)
        z = pi_o_2 + 0.5 * pi_lo; /* |y/x| >  2**60 */
    else if (hx < 0 && k < -60)
        z = 0.0; /* |y|/x < -2**60 */
    else
        z = atan(fabs(y / x)); /* safe to do y/x */
    switch (m)
    {
    case 0:
        return z; /* atan(+,+) */
    case 1:
    {
        uint32_t zh;
        GET_HIGH_WORD(zh, z);
        SET_HIGH_WORD(z, zh ^ 0x80000000);
    }
        return z; /* atan(-,+) */
    case 2:
        return pi - (z - pi_lo); /* atan(+,-) */
    default:                     /* case 3 */
        return (z - pi_lo) - pi; /* atan(-,-) */
    }
}

Here is the call graph for this function:

Here is the caller graph for this function:

atanh()

double atanh

(

double

x

)

Inverse hyperbolic tangent function.

Method
1.Reduced x to positive by atanh(-x) = -atanh(x)
2.For x>=0.5
              1               2x                         x
  atanh(x) = --- * log(1 + -------) = 0.5 * log1p(2 * --------)
              2             1 - x                      1 - x

  For x<0.5
  atanh(x) = 0.5*log1p(2x+2x*x/(1-x))

Special cases
    atanh(x) is NaN if |x| > 1
    atanh(NaN) is that NaN
    atanh(+-1) is +-INF

Definition at line 72 of file atanh.c.

References huge, log1p(), one, and zero.

Referenced by RealNumber::HypArcTangent().

{
    double t;
    int32_t hx, ix;
    uint32_t lx;
    GET_HIGH_WORD(hx, x);
    GET_LOW_WORD(lx, x);
    ix = hx & 0x7FFFFFFF;

    // |x| > 1
    if ((ix | ((lx | (-lx)) >> 31)) > 0x3FF00000)
    {
        return NAN;
    }

    if (ix == 0x3FF00000)
        return x / zero;
    if (ix < 0x3E300000 && (huge + x) > zero)
        return x;         /* x<2**-28 */
    SET_HIGH_WORD(x, ix); /* x <- |x| */
    if (ix < 0x3FE00000)
    { /* x < 0.5 */
        t = x + x;
        t = 0.5 * log1p(t + t * x / (one - x));
    }
    else
        t = 0.5 * log1p((x + x) / (one - x));

    if (hx >= 0)
    {
        return t;
    }

    return -t;
}

Here is the call graph for this function:

Here is the caller graph for this function:

avcs()

double avcs

(

double

x

)

Inverse versed sine.

avcs(x) = acos(1+x)

Definition at line 44 of file avcs.c.

References acos().

Referenced by RealNumber::ArcVerCosine().

{
    return acos(1.0 + x);
}

Here is the call graph for this function:

Here is the caller graph for this function:

aver()

double aver

(

double

x

)

Inverse versed sine function.

Definition at line 40 of file aver.c.

References atan(), and sqrt().

Referenced by RealNumber::ArcVerSine().

{
    double a, b, c, d;

    if (x < 0.0 || x > 2.0)
    {
        return NAN;
    }

    a = 2.0 * x - x * x;
    b = sqrt(a);
    c = 1.0 - x;

    if (TRIG_INEXACT(c))
    {
        return INFP;
    }

    d = atan(b / c);
    return d;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cbrt()

double cbrt

(

double

x

)

Cube root function.

Definition at line 62 of file cbrt.c.

References B1, B2, C, D, E, F, and G.

Referenced by RealNumber::CubeRoot().

{
    int32_t hx, lx, ht;
    double r, s, t = 0.0, w;
    uint32_t sign;

    GET_HIGH_WORD(hx, x);

    // sign = sign(x)
    sign = hx & 0x80000000;
    hx ^= sign;

    // cbrt(NaN,INF) is itself
    if (hx >= 0x7FF00000)
    {
        return x + x;
    }

    GET_LOW_WORD(lx, x);

    // cbrt(0) is itself
    if ((hx | lx) == 0)
    {
        return x;
    }

    // x <- |x|
    SET_HIGH_WORD(x, hx);

    // rough cbrt to 5 bits
    if (hx < 0x00100000) // subnormal number
    {
        SET_HIGH_WORD(t, 0x43500000); // set t= 2**54
        t *= x;
        GET_HIGH_WORD(ht, t);
        SET_HIGH_WORD(t, ht / 3 + B2);
    }
    else
    {
        SET_HIGH_WORD(t, hx / 3 + B1);
    }

    // new cbrt to 23 bits, may be implemented in single precision
    r = t * t / x;
    s = C + r * t;
    t *= G + F / (s + E + D / s);

    // chopped to 20 bits and make it larger than cbrt(x)
    SET_LOW_WORD(t, 0);
    GET_HIGH_WORD(ht, t);
    SET_HIGH_WORD(t, ht + 0x00000001);

    // one step newton iteration to 53 bits with error less than 0.667 ulps
    s = t * t; // t*t is exact
    r = x / s;
    w = t + t;
    r = (r - t) / (w + r); // r-s is exact
    t = t + t * r;

    // retore the sign bit
    GET_HIGH_WORD(ht, t);
    SET_HIGH_WORD(t, ht | sign);

    return (t);
}

Here is the caller graph for this function:

ceil()

double ceil

(

double

x

)

Ceiling function.

Parameters

x

Returns

x rounded toward -inf to integral value

Method
    Bit twiddling

Exception
    Inexact flag raised if x not equal to ceil(x).

Definition at line 63 of file ceil.c.

References huge.

Referenced by cceil(), RealNumber::Ceiling(), Dragon4(), round(), and trunc().

{
    int32_t i0,i1,j0;
    uint32_t i,j;
    EXTRACT_WORDS(i0,i1,x);
    j0 = ((i0>>20)&0x7ff)-0x3ff;
    if(j0<20) {
        if(j0<0) {          /* raise inexact if x != 0 */
            if(huge+x>0.0) {        /* return 0*sign(x) if |x|<1 */
                if(i0<0) {
                    i0=0x80000000;
                    i1=0;
                }
                else if((i0|i1)!=0) {
                    i0=0x3ff00000;
                    i1=0;
                }
            }
        } else {
            i = (0x000fffff)>>j0;
            if(((i0&i)|i1)==0) return x; /* x is integral */
            if(huge+x>0.0) {        /* raise inexact flag */
                if(i0>0) i0 += (0x00100000)>>j0;
                i0 &= (~i);
                i1=0;
            }
        }
    } else if (j0>51) {
        if(j0==0x400) return x+x;   /* inf or NaN */
        else return x;          /* x is integral */
    } else {
        i = ((uint32_t)(0xffffffff))>>(j0-20);
        if((i1&i)==0) return x;     /* x is integral */
        if(huge+x>0.0) {        /* raise inexact flag */
            if(i0>0) {
                if(j0==20) i0+=1;
                else {
                    j = i1 + (1<<(52-j0));
                    // NOTICE: Is this a correct cast?
                    if((int32_t)j<(int32_t)i1) i0+=1;   /* got a carry */
                    i1 = j;
                }
            }
            i1 &= (~i);
        }
    }
    INSERT_WORDS(x,i0,i1);
    return x;
}

Here is the caller graph for this function:

copysign()

double copysign	(	double	x,
		double	y
	)

Returns a value with the magnitude of x and with the sign bit of y.

Definition at line 47 of file csign.c.

Referenced by scalbn().

{
    uint32_t hx, hy;
    GET_HIGH_WORD(hx, x);
    GET_HIGH_WORD(hy, y);
    SET_HIGH_WORD(x, (hx & 0x7fffffff) | (hy & 0x80000000));
    return x;
}

Here is the caller graph for this function:

cos()

double cos

(

double

x

)

Cosine function.

Parameters

x

Returns

Cosine function of x

Kernel function:
__kernel_sin        ... sine function on [-pi/4,pi/4]
__kernel_cos        ... cose function on [-pi/4,pi/4]
__ieee754_rem_pio2  ... argument reduction routine

Method:
Let S,C and T denote the sin, cos and tan respectively on
[-PI/4, +PI/4]. Reduce the argument x to y1+y2 = x-k*pi/2
in [-pi/4 , +pi/4], and let n = k mod 4.

We have

     n        sin(x)      cos(x)        tan(x)
----------------------------------------------------------
     0          S           C             T
     1          C          -S           -1/T
     2         -S          -C             T
     3         -C           S           -1/T
----------------------------------------------------------

Special cases:
Let trig be any of sin, cos, or tan.
trig(+-INF)  is NaN
trig(NaN)    is that NaN

Accuracy:
TRIG(x) returns trig(x) nearly rounded

Definition at line 87 of file cos.c.

References __kernel_cos(), __kernel_sin(), and rempio2().

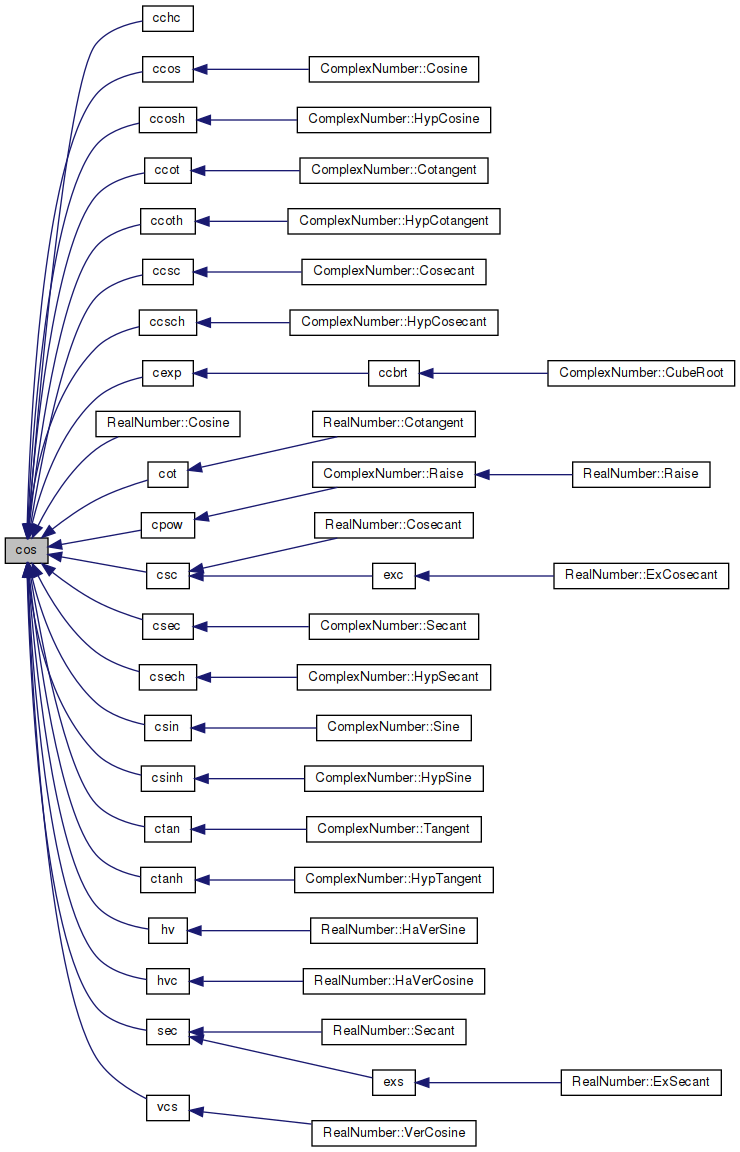
Referenced by cchc(), ccos(), ccosh(), ccot(), ccoth(), ccsc(), ccsch(), cexp(), RealNumber::Cosine(), cot(), cpow(), csc(), csec(), csech(), csin(), csinh(), ctan(), ctanh(), hv(), hvc(), sec(), and vcs().

{
    double y[2], z = 0.0;
    int32_t n, ix;

    // High word of x
    GET_HIGH_WORD(ix, x);
    ix &= 0x7FFFFFFF;

    // |x| ~< pi/4
    if (ix <= 0x3FE921FB)
    {
        return __kernel_cos(x, z);
    }

    // cos(Inf or NaN) is NaN
    if (ix >= 0x7FF00000)
    {
        return NAN;
    }

    // argument reduction needed
    n = rempio2(x, y);
    switch (n & 3)
    {
    case 0:
        return __kernel_cos(y[0], y[1]);
    case 1:
        return -__kernel_sin(y[0], y[1], 1);
    case 2:
        return -__kernel_cos(y[0], y[1]);
    default:
        return __kernel_sin(y[0], y[1], 1);
    }
}

Here is the call graph for this function:

Here is the caller graph for this function:

cosh()

double cosh

(

double

x

)

Hyperbolic cosine function.

Mathematically cosh(x) if defined to be (exp(x)+exp(-x))/2

Method
1. Replace x by |x| (cosh(x) = cosh(-x))
2.
                                              [ exp(x) - 1 ]^2
   0        <= x <= ln2/2  :  cosh(x) := 1 + -------------------
                                                2*exp(x)

                                         exp(x) +  1/exp(x)
   ln2/2    <= x <= 22     :  cosh(x) := -------------------
                                                 2
   22       <= x <= lnovft :  cosh(x) := exp(x)/2
   lnovft   <= x <= ln2ovft:  cosh(x) := exp(x/2)/2 * exp(x/2)
   ln2ovft  <  x           :  cosh(x) := huge*huge (overflow)

Special cases:
cosh(x) is |x| if x is +INF, -INF, or NaN
only cosh(0)=1 is exact for finite x

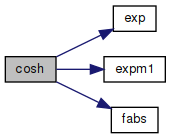
Definition at line 83 of file cosh.c.

References exp(), expm1(), fabs(), half, huge, and one.

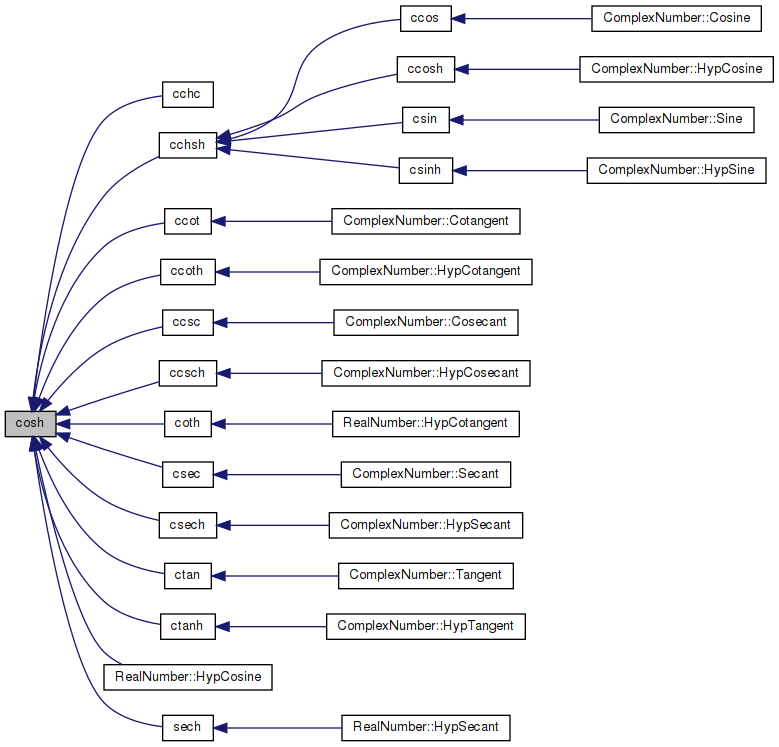
Referenced by cchc(), cchsh(), ccot(), ccoth(), ccsc(), ccsch(), coth(), csec(), csech(), ctan(), ctanh(), RealNumber::HypCosine(), and sech().

{
    double t, w;
    int32_t ix;
    uint32_t lx;

    // High word of |x|
    GET_HIGH_WORD(ix, x);
    ix &= 0x7FFFFFFF;

    // x is INF or NaN
    if (ix >= 0x7FF00000)
    {
        return x * x;
    }

    // |x| in [0,0.5*ln2]
    if (ix < 0x3FD62E43)
    {
        t = expm1(fabs(x));
        w = one + t;
        if (ix < 0x3C800000)
        {
            // cosh(tiny) = 1
            return w;
        }

        return one + (t * t) / (w + w);
    }

    // |x| in [0.5*ln2,22]
    if (ix < 0x40360000)
    {
        t = exp(fabs(x));
        return half * t + half / t;
    }

    // |x| in [22, log(maxdouble)]
    if (ix < 0x40862E42)
    {
        return half * exp(fabs(x));
    }

    // |x| in [log(maxdouble), overflowthresold]
    lx = *((((*(unsigned *)&one) >> 29)) + (unsigned *)&x);
    if (ix < 0x408633CE || ((ix == 0x408633CE) && (lx <= (unsigned)0x8FB9F87D)))
    {
        w = exp(half * fabs(x));
        t = half * w;
        return t * w;
    }

    // |x| > overflowthresold, cosh(x) overflow
    return huge * huge;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cot()

double cot

(

double

x

)

Cotangent function.

Parameters

x

cot(x) = 1/tan(x)
       = cos(x)/sin(x)
       = sin(2*x)/(cos(2*x)-1)

Definition at line 47 of file cot.c.

References cos(), and sin().

Referenced by RealNumber::Cotangent().

{
    double a, b, c;

    a = cos(x);
    b = sin(x);

    if (TRIG_INEXACT(b))
    {
        return NAN;
    }

    c = a / b;
    return c;
}

Here is the call graph for this function:

Here is the caller graph for this function:

coth()

double coth

(

double

x

)

Hyperbolic cotangent function.

coth(x) = cosh(x)/sinh(x)

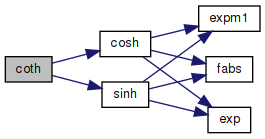
Definition at line 44 of file coth.c.

References cosh(), and sinh().

Referenced by RealNumber::HypCotangent().

{
    double a, b, c;

    a = cosh(x);
    b = sinh(x);

    if (TRIG_INEXACT(b))
    {
        return NAN;
    }

    c = a / b;
    return c;
}

Here is the call graph for this function:

Here is the caller graph for this function:

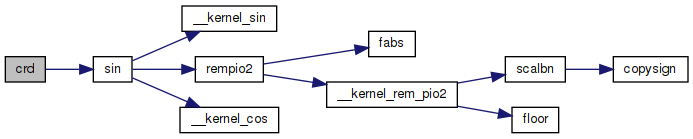
crd()

double crd

(

double

x

)

Chord function.

crd(x) = 2*sin(x/2)

Definition at line 44 of file crd.c.

References sin().

Referenced by RealNumber::Chord().

{
    double a = x / 2.0;
    double b = sin(a);
    double c = 2.0 * b;
    return c;
}

Here is the call graph for this function:

Here is the caller graph for this function:

csc()

double csc

(

double

x

)

Cosecant function.

csc = sin(1/x)
    = -2*sin(x)/(cos(2*x) - 1)

Definition at line 45 of file csc.c.

References cos(), and sin().

Referenced by RealNumber::Cosecant(), and exc().

{
    double a, b, c;

    b = cos(2.0 * x) - 1.0;
    if (b == 0.0)
    {
        return NAN;
    }

    a = -2.0 * sin(x);
    c = a / b;
    return c;
}

Here is the call graph for this function:

Here is the caller graph for this function:

csch()

double csch

(

double

x

)

Hyperbolic cosecant function.

csch(x) = 1/sinh(x)

Definition at line 44 of file csch.c.

References sinh().

Referenced by RealNumber::HypCosecant().

{
    double a = sinh(x);
    if (TRIG_INEXACT(a))
    {
        return NAN;
    }
    return 1.0 / a;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cvc()

double cvc

(

double

x

)

Coversed cosine function.

cvc(x) = 1+sin(x)

Definition at line 44 of file cvc.c.

References sin().

Referenced by RealNumber::CoVerCosine().

{
    return 1.0 + sin(x);
}

Here is the call graph for this function:

Here is the caller graph for this function:

cvs()

double cvs

(

double

x

)

Coversed sine function.

cvs(x) = 1-sin(x)

Definition at line 44 of file cvs.c.

References sin().

Referenced by RealNumber::CoVerSine(), and exc().

{
    return 1.0 - sin(x);
}

Here is the call graph for this function:

Here is the caller graph for this function:

exc()

double exc

(

double

x

)

Excosecant function.

excsc(x) = csc(x)-1
         = (1-sin(x))/sin(x)
         = cvs(x)/sin(x)
         = cvs(x)*csc(x)

Definition at line 47 of file exc.c.

References csc(), and cvs().

Referenced by RealNumber::ExCosecant().

{
    return cvs(x) * csc(x);
}

Here is the call graph for this function:

Here is the caller graph for this function:

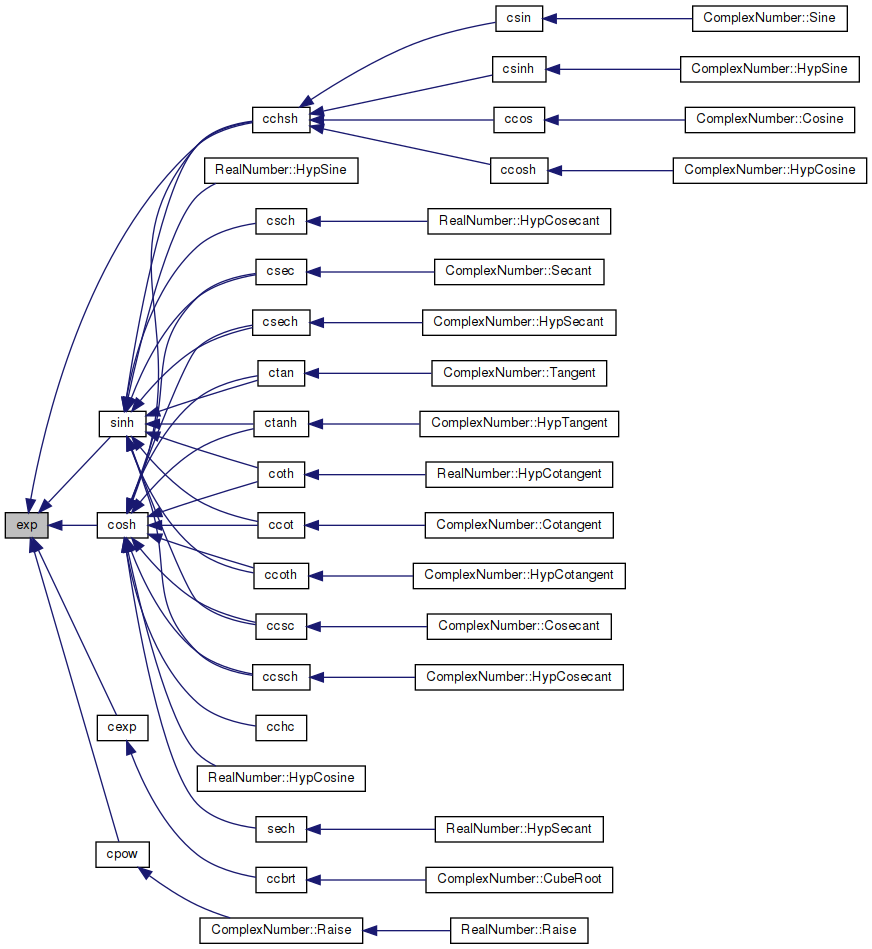
exp()

double exp

(

double

x

)

Returns the exponential of x.

Method
1. Argument reduction:
   Reduce x to an r so that |r| <= 0.5*ln2 ~ 0.34658.
   Given x, find r and integer k such that

           x = k*ln2 + r,  |r| <= 0.5*ln2.

   Here r will be represented as r = hi-lo for better
   accuracy.

2. Approximation of exp(r) by a special rational function on
   the interval [0,0.34658]:

   Write
       R(r**2) = r*(exp(r)+1)/(exp(r)-1) = 2 + r*r/6 - r**4/360 + ...
   We use a special Remes algorithm on [0,0.34658] to generate
   a polynomial of degree 5 to approximate R. The maximum error
   of this polynomial approximation is bounded by 2**-59. In
   other words,
       R(z) ~ 2.0 + P1*z + P2*z**2 + P3*z**3 + P4*z**4 + P5*z**5
       (where z=r*r, and the values of P1 to P5 are listed below)
   and

       |                  5          |     -59
       | 2.0+P1*z+...+P5*z   -  R(z) | <= 2
       |                             |

   The computation of exp(r) thus becomes
                      2*r
       exp(r) = 1 + -------
                     R - r
                          r*R1(r)
              = 1 + r + ----------- (for better accuracy)
                         2 - R1(r)
   where
                2       4                     10
       R1(r) = r - (P1*r  + P2*r  + ... + P5*r   ).

3. Scale back to obtain exp(x):
   From step 1, we have
   exp(x) = 2^k * exp(r)

Special cases:
exp(INF) is INF, exp(NaN) is NaN;
exp(-INF) is 0, and
for finite argument, only exp(0)=1 is exact.

Accuracy:
according to an error analysis, the error is always less than
1 ulp (unit in the last place).

Misc. info:
For IEEE double
    if x >  7.09782712893383973096e+02 then exp(x) overflow
    if x < -7.45133219101941108420e+02 then exp(x) underflow

Constants:

The hexadecimal values are the intended ones for the following
constants. The decimal values may be used, provided that the
compiler will convert from decimal to binary accurately enough
to produce the hexadecimal values shown.

Definition at line 138 of file exp.c.

References halF, huge, invln2, ln2HI, ln2LO, o_threshold, one, P1, P2, P3, P4, P5, twom1000, and u_threshold.

Referenced by cchsh(), cexp(), cosh(), cpow(), and sinh().

{
    double y, hi, lo, c, t;
    int32_t k, xsb;
    uint32_t hx, hy;

    lo = 0.0;
    hi = 0.0;

    GET_HIGH_WORD(hx, x); // high word of x
    xsb = (hx >> 31) & 1; // sign bit of x
    hx &= 0x7FFFFFFF;     // high word of |x|

    // filter out non-finite argument
    // if |x|>=709.78...
    if (hx >= 0x40862E42)
    {
        if (hx >= 0x7FF00000)
        {
            uint32_t lx;
            GET_LOW_WORD(lx, x);
            if (((hx & 0xFFFFF) | lx) != 0)
            {
                return NAN;
            }

            // exp(+-inf)={inf,0}
            return (xsb == 0) ? x : 0.0;
        }

        if (x > o_threshold)
        {
            // overflow
            return huge * huge;
        }

        if (x < u_threshold)
        {
            // underflow
            return twom1000 * twom1000;
        }
    }

    // argument reduction
    // |x| > 0.5 ln2
    if (hx > 0x3FD62E42)
    {
        // |x| < 1.5 ln2
        if (hx < 0x3FF0A2B2)
        {
            hi = x - ln2HI[xsb];
            lo = ln2LO[xsb];
            k = 1 - xsb - xsb;
        }
        else
        {
            k = (int32_t)(invln2 * x + halF[xsb]);
            t = k;
            hi = x - t * ln2HI[0]; // t*ln2HI is exact here
            lo = t * ln2LO[0];
        }
        x = hi - lo;
    }
    // when |x|<2**-28
    else if (hx < 0x3E300000)
    {
        if (huge + x > one)
        {
            return one + x; // trigger inexact
        }
        else
        {
            k = 0;
        }
    }
    else
    {
        k = 0;
    }

    // x is now in primary range
    t = x * x;
    c = x - t * (P1 + t * (P2 + t * (P3 + t * (P4 + t * P5))));
    if (k == 0)
    {
        return one - ((x * c) / (c - 2.0) - x);
    }

    y = one - ((lo - (x * c) / (2.0 - c)) - hi);

    if (k >= -1021)
    {
        GET_HIGH_WORD(hy, y);
        SET_HIGH_WORD(y, hy + (k << 20)); // add k to y's exponent
        return y;
    }

    GET_HIGH_WORD(hy, y);
    SET_HIGH_WORD(y, hy + ((k + 1000) << 20)); // add k to y's exponent
    return y * twom1000;
}

Here is the caller graph for this function:

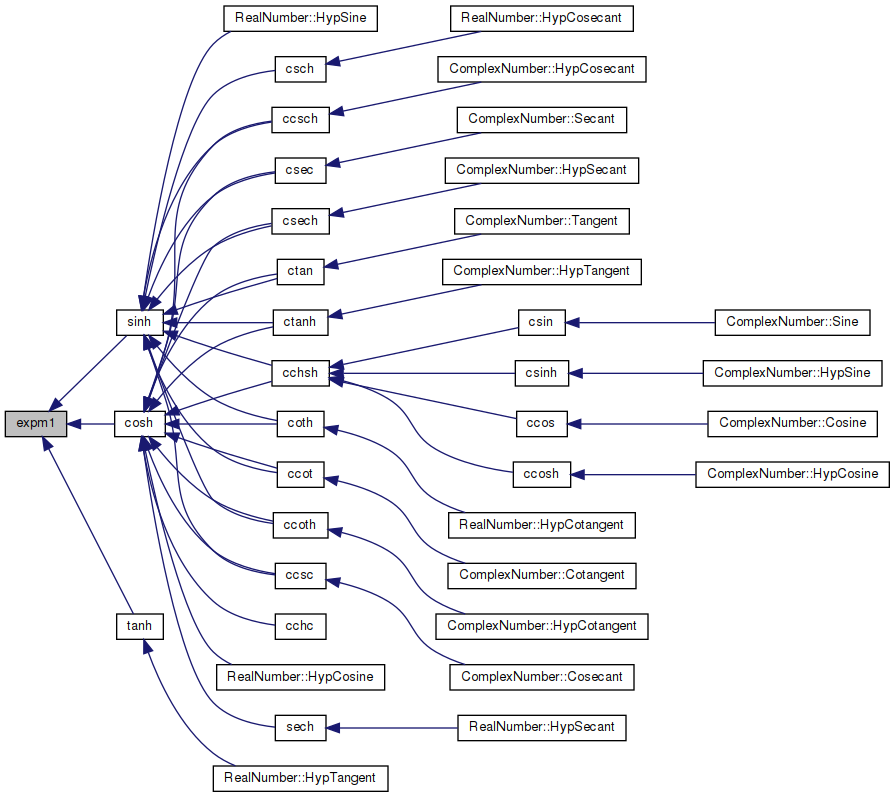
expm1()

double expm1

(

double

x

)

Definition at line 153 of file expm1.c.

References huge, invln2, ln2_hi, ln2_lo, o_threshold, one, Q1, Q2, Q3, Q4, Q5, and tiny.

Referenced by cosh(), sinh(), and tanh().

{
    double y, hi, lo, c, t, e, hxs, hfx, r1;
    int32_t k, xsb;
    uint32_t hx;

    c = 0.0;

    GET_HIGH_WORD(hx, x);  /* high word of x */
    xsb = hx & 0x80000000; /* sign bit of x */
    hx &= 0x7fffffff; /* high word of |x| */

    /* filter out huge and non-finite argument */
    if (hx >= 0x4043687A)
    { /* if |x|>=56*ln2 */
        if (hx >= 0x40862E42)
        { /* if |x|>=709.78... */
            if (hx >= 0x7ff00000)
            {
                uint32_t low;
                GET_LOW_WORD(low, x);
                if (((hx & 0xfffff) | low) != 0)
                    return x + x; /* NaN */
                else
                    return (xsb == 0) ? x : -1.0; /* exp(+-inf)={inf,-1} */
            }
            if (x > o_threshold)
                return huge * huge; /* overflow */
        }
        if (xsb != 0)
        {                          /* x < -56*ln2, return -1.0 with inexact */
            if (x + tiny < 0.0)    /* raise inexact */
                return tiny - one; /* return -1 */
        }
    }

    /* argument reduction */
    if (hx > 0x3fd62e42)
    { /* if  |x| > 0.5 ln2 */
        if (hx < 0x3FF0A2B2)
        { /* and |x| < 1.5 ln2 */
            if (xsb == 0)
            {
                hi = x - ln2_hi;
                lo = ln2_lo;
                k = 1;
            }
            else
            {
                hi = x + ln2_hi;
                lo = -ln2_lo;
                k = -1;
            }
        }
        else
        {
            k = (int32_t)(invln2 * x + ((xsb == 0) ? 0.5 : -0.5));
            t = k;
            hi = x - t * ln2_hi; /* t*ln2_hi is exact here */
            lo = t * ln2_lo;
        }
        x = hi - lo;
        c = (hi - x) - lo;
    }
    else if (hx < 0x3c900000)
    {                 /* when |x|<2**-54, return x */
        t = huge + x; /* return x with inexact flags when x!=0 */
        return x - (t - (huge + x));
    }
    else
        k = 0;

    /* x is now in primary range */
    hfx = 0.5 * x;
    hxs = x * hfx;
    r1 = one + hxs * (Q1 + hxs * (Q2 + hxs * (Q3 + hxs * (Q4 + hxs * Q5))));
    t = 3.0 - r1 * hfx;
    e = hxs * ((r1 - t) / (6.0 - x * t));
    if (k == 0)
        return x - (x * e - hxs); /* c is 0 */
    else
    {
        e = (x * (e - c) - c);
        e -= hxs;
        if (k == -1)
            return 0.5 * (x - e) - 0.5;
        if (k == 1)
        {
            if (x < -0.25)
                return -2.0 * (e - (x + 0.5));
            else
                return one + 2.0 * (x - e);
        }
        if (k <= -2 || k > 56)
        { /* suffice to return exp(x)-1 */
            uint32_t hy;

            y = one - (e - x);
            GET_HIGH_WORD(hy, y);
            SET_HIGH_WORD(y, hy + (k << 20)); /* add k to y's exponent */
            return y - one;
        }
        t = one;
        if (k < 20)
        {
            uint32_t hy;

            SET_HIGH_WORD(t, 0x3ff00000 - (0x200000 >> k)); /* t=1-2^-k */
            y = t - (e - x);
            GET_HIGH_WORD(hy, y);
            SET_HIGH_WORD(y, hy + (k << 20)); /* add k to y's exponent */
        }
        else
        {
            uint32_t hy;

            SET_HIGH_WORD(t, (0x3ff - k) << 20); /* 2^-k */
            y = x - (e + t);
            y += one;
            GET_HIGH_WORD(hy, y);
            SET_HIGH_WORD(y, hy + (k << 20)); /* add k to y's exponent */
        }
    }
    return y;
}

Here is the caller graph for this function:

exs()

double exs

(

double

x

)

Exsecant function.

exsec(x) = sec(x)-1
         = (1-cos(x))/cos(x)
         = ver(x)/cos(x)
         = ver(x)*sec(x)
         = 2*sin(x/2)*sin(x/2)*sec(x)

Definition at line 48 of file exs.c.

References sec(), and ver().

Referenced by RealNumber::ExSecant().

{
    return ver(x) * sec(x);
}

Here is the call graph for this function:

Here is the caller graph for this function:

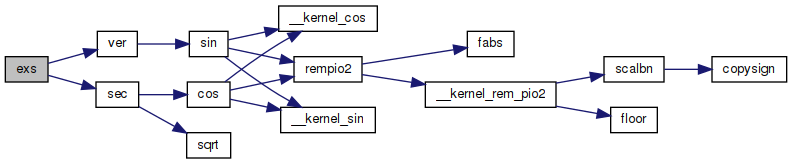
fabs()

double fabs

(

double

x

)

Returns the absolute value of x.

Definition at line 51 of file fabs.c.

Referenced by __kernel_tan(), RealNumber::Absolute(), asin(), asinh(), atan(), atan2(), cchsh(), cosh(), csqrt(), DecimalSystem::GetText(), PositionalNumeralSystem::GetText(), pow(), rempio2(), sinh(), and tanh().

{
    uint32_t hx;
    GET_HIGH_WORD(hx, x);
    SET_HIGH_WORD(x, hx & 0x7fffffff);
    return x;
}

Here is the caller graph for this function:

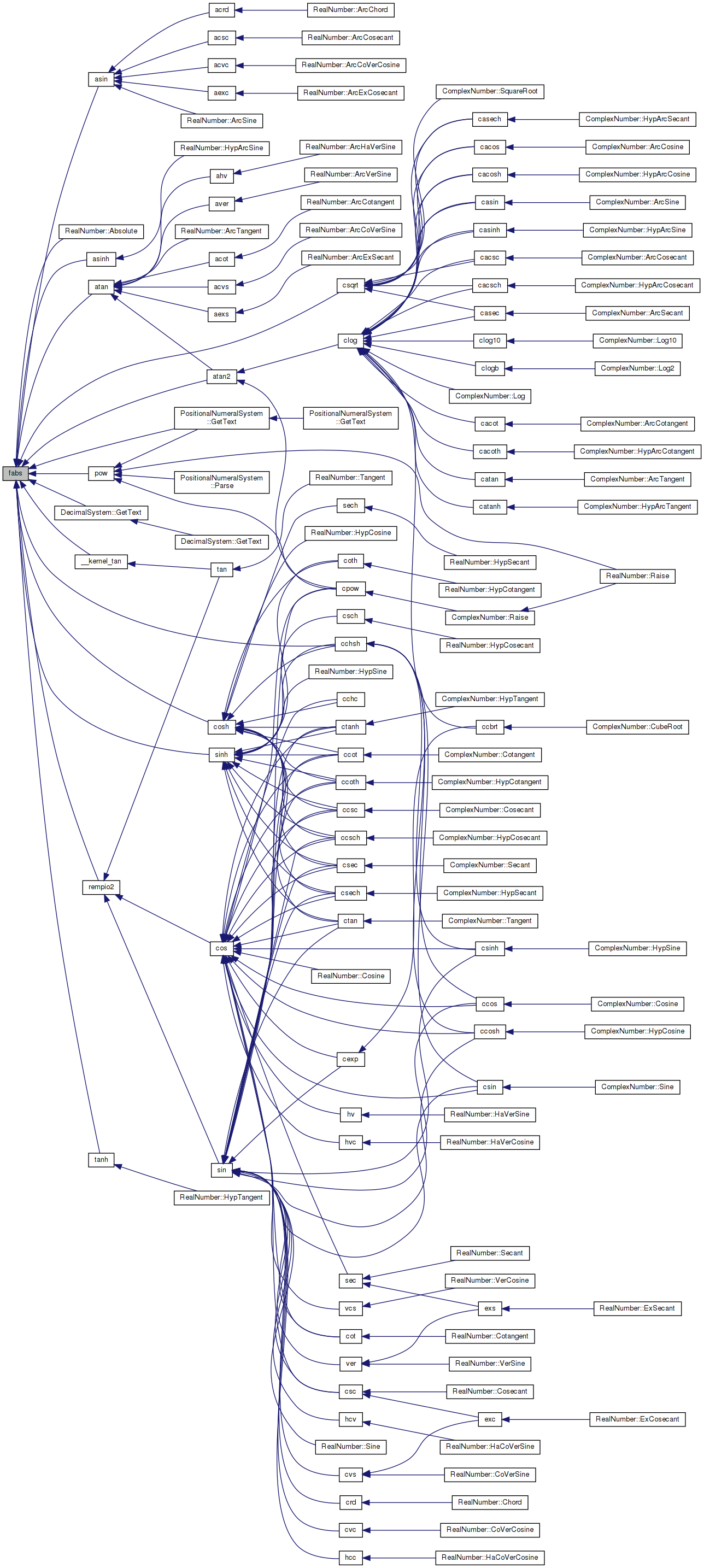
floor()

double floor

(

double

x

)

Floor function.

Returns

x rounded toward -inf to integral value

Method:
    Bit twiddling

Exception:
    Inexact flag raised if x not equal to floor(x)

Definition at line 62 of file floor.c.

References huge.

Referenced by __kernel_rem_pio2(), cfloor(), RealNumber::Floor(), round(), and trunc().

{
    int32_t i0, i1, j0;
    uint32_t i, j;
    EXTRACT_WORDS(i0, i1, x);
    j0 = ((i0 >> 20) & 0x7ff) - 0x3ff;
    if (j0 < 20)
    {
        if (j0 < 0)
        { /* raise inexact if x != 0 */
            if (huge + x > 0.0)
            { /* return 0*sign(x) if |x|<1 */
                if (i0 >= 0)
                {
                    i0 = i1 = 0;
                }
                else if (((i0 & 0x7fffffff) | i1) != 0)
                {
                    i0 = 0xbff00000;
                    i1 = 0;
                }
            }
        }
        else
        {
            i = (0x000fffff) >> j0;
            if (((i0 & i) | i1) == 0)
                return x; /* x is integral */
            if (huge + x > 0.0)
            { /* raise inexact flag */
                if (i0 < 0)
                    i0 += (0x00100000) >> j0;
                i0 &= (~i);
                i1 = 0;
            }
        }
    }
    else if (j0 > 51)
    {
        if (j0 == 0x400)
            return x + x; /* inf or NaN */
        else
            return x; /* x is integral */
    }
    else
    {
        i = ((uint32_t)(0xffffffff)) >> (j0 - 20);
        if ((i1 & i) == 0)
            return x; /* x is integral */
        if (huge + x > 0.0)
        { /* raise inexact flag */
            if (i0 < 0)
            {
                if (j0 == 20)
                    i0 += 1;
                else
                {
                    j = i1 + (1 << (52 - j0));
                    if (j < (uint32_t)i1)
                        i0 += 1; /* got a carry */
                    i1 = j;
                }
            }
            i1 &= (~i);
        }
    }
    INSERT_WORDS(x, i0, i1);
    return x;
}

Here is the caller graph for this function:

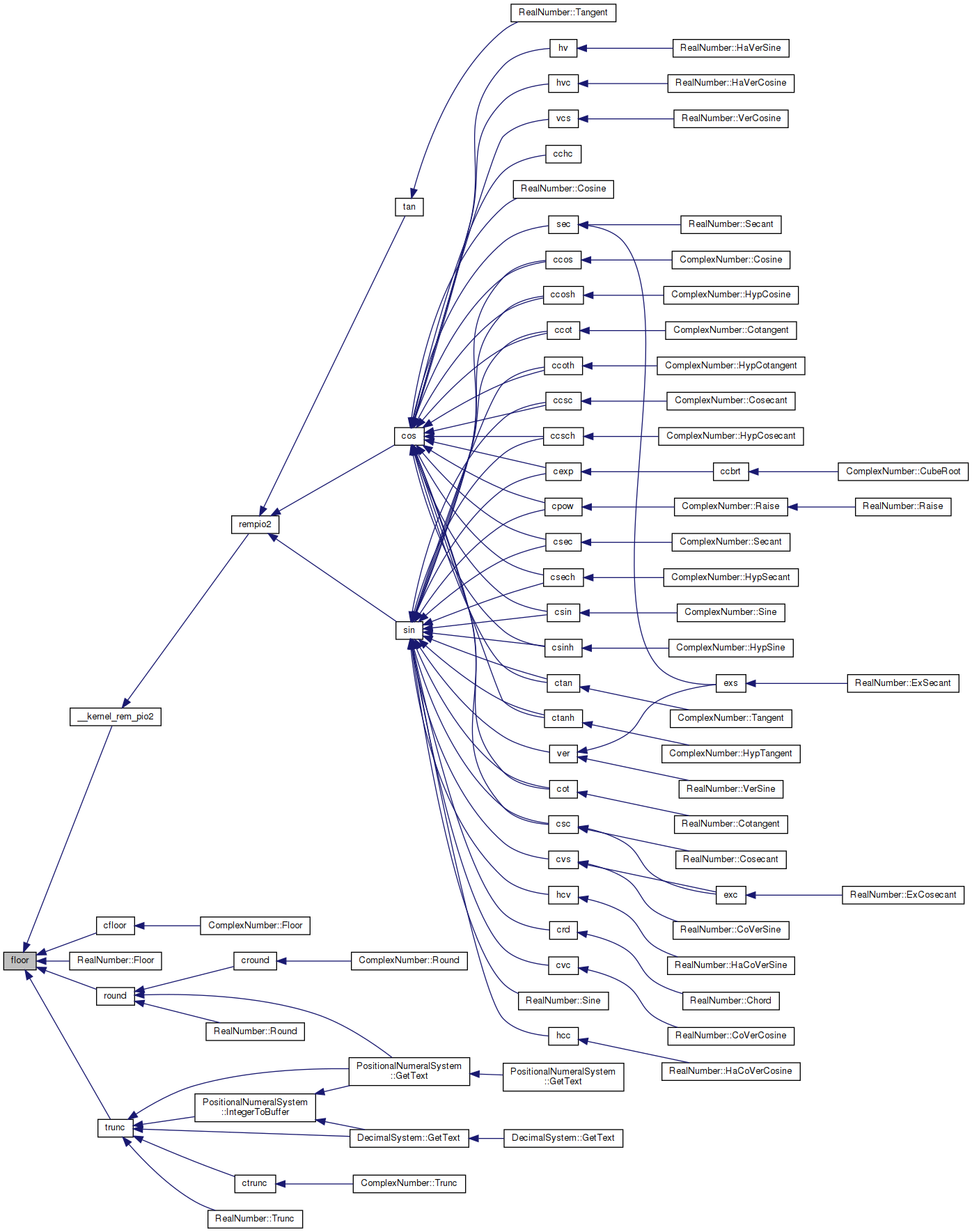
fmod()

double fmod	(	double	x,
		double	y
	)

Return x mod y in exact arithmetic.

Method: Shift and subtract

Definition at line 58 of file fmod.c.

References one, and Zero.

Referenced by PositionalNumeralSystem::IntegerToBuffer().

{
    int32_t n, hx, hy, hz, ix, iy, sx, i;
    uint32_t lx, ly, lz;

    EXTRACT_WORDS(hx, lx, x);
    EXTRACT_WORDS(hy, ly, y);
    sx = hx & 0x80000000; /* sign of x */
    hx ^= sx;             /* |x| */
    hy &= 0x7fffffff;     /* |y| */

    /* purge off exception values */
    if ((hy | ly) == 0 || (hx >= 0x7ff00000) ||   /* y=0,or x not finite */
        ((hy | ((ly | -ly) >> 31)) > 0x7ff00000)) /* or y is NaN */
        return (x * y) / (x * y);
    if (hx <= hy)
    {
        if ((hx < hy) || (lx < ly))
            return x; /* |x|<|y| return x */
        if (lx == ly)
            return Zero[(uint32_t)sx >> 31]; /* |x|=|y| return x*0*/
    }

    /* determine ix = ilogb(x) */
    if (hx < 0x00100000)
    { /* subnormal x */
        if (hx == 0)
        {
            for (ix = -1043, i = lx; i > 0; i <<= 1)
                ix -= 1;
        }
        else
        {
            for (ix = -1022, i = (hx << 11); i > 0; i <<= 1)
                ix -= 1;
        }
    }
    else
        ix = (hx >> 20) - 1023;

    /* determine iy = ilogb(y) */
    if (hy < 0x00100000)
    { /* subnormal y */
        if (hy == 0)
        {
            for (iy = -1043, i = ly; i > 0; i <<= 1)
                iy -= 1;
        }
        else
        {
            for (iy = -1022, i = (hy << 11); i > 0; i <<= 1)
                iy -= 1;
        }
    }
    else
        iy = (hy >> 20) - 1023;

    /* set up {hx,lx}, {hy,ly} and align y to x */
    if (ix >= -1022)
        hx = 0x00100000 | (0x000fffff & hx);
    else
    { /* subnormal x, shift x to normal */
        n = -1022 - ix;
        if (n <= 31)
        {
            hx = (hx << n) | (lx >> (32 - n));
            lx <<= n;
        }
        else
        {
            hx = lx << (n - 32);
            lx = 0;
        }
    }
    if (iy >= -1022)
        hy = 0x00100000 | (0x000fffff & hy);
    else
    { /* subnormal y, shift y to normal */
        n = -1022 - iy;
        if (n <= 31)
        {
            hy = (hy << n) | (ly >> (32 - n));
            ly <<= n;
        }
        else
        {
            hy = ly << (n - 32);
            ly = 0;
        }
    }

    /* fix point fmod */
    n = ix - iy;
    while (n--)
    {
        hz = hx - hy;
        lz = lx - ly;
        if (lx < ly)
            hz -= 1;
        if (hz < 0)
        {
            hx = hx + hx + (lx >> 31);
            lx = lx + lx;
        }
        else
        {
            if ((hz | lz) == 0) /* return sign(x)*0 */
                return Zero[(uint32_t)sx >> 31];
            hx = hz + hz + (lz >> 31);
            lx = lz + lz;
        }
    }
    hz = hx - hy;
    lz = lx - ly;
    if (lx < ly)
        hz -= 1;
    if (hz >= 0)
    {
        hx = hz;
        lx = lz;
    }

    /* convert back to floating value and restore the sign */
    if ((hx | lx) == 0) /* return sign(x)*0 */
        return Zero[(unsigned)sx >> 31];
    while (hx < 0x00100000)
    { /* normalize x */
        hx = hx + hx + (lx >> 31);
        lx = lx + lx;
        iy -= 1;
    }
    if (iy >= -1022)
    { /* normalize output */
        hx = ((hx - 0x00100000) | ((iy + 1023) << 20));
        INSERT_WORDS(x, hx | sx, lx);
    }
    else
    { /* subnormal output */
        n = -1022 - iy;
        if (n <= 20)
        {
            lx = (lx >> n) | ((uint32_t)hx << (32 - n));
            hx >>= n;
        }
        else if (n <= 31)
        {
            lx = (hx << (32 - n)) | (lx >> n);
            hx = sx;
        }
        else
        {
            lx = hx >> (n - 32);
            hx = sx;
        }
        INSERT_WORDS(x, hx | sx, lx);
        x *= one; /* create necessary signal */
    }
    return x; /* exact output */
}

Here is the caller graph for this function:

hcc()

double hcc

(

double

x

)

Hacoversed cosine function.

hcc(x) = (1+sin(x))/2

Definition at line 44 of file hcc.c.

References sin().

Referenced by RealNumber::HaCoVerCosine().

{
    double a = sin(x);
    double b = 1.0 - a;
    double c = b / 2.0;
    return c;
}

Here is the call graph for this function:

Here is the caller graph for this function:

hcv()

double hcv

(

double

x

)

Hacoversed sine function.

hcv(x) = (1-sin(x))/2

Definition at line 44 of file hcv.c.

References sin().

Referenced by RealNumber::HaCoVerSine().

{
    double a = sin(x);
    double b = 1.0 - a;
    double c = b / 2.0;
    return c;
}

Here is the call graph for this function:

Here is the caller graph for this function:

hv()

double hv

(

double

x

)

Haversed sine function.

hv(x) = (1-cos(x))/2

Definition at line 44 of file hv.c.

References cos().

Referenced by RealNumber::HaVerSine().

{
    double a = cos(x);
    double b = 1.0 - a;
    double c = b / 2.0;
    return c;
}

Here is the call graph for this function:

Here is the caller graph for this function:

hvc()

double hvc

(

double

x

)

Haversed cosine function.

hvc(x) = (1+cos(x))/2

Definition at line 44 of file hvc.c.

References cos().

Referenced by RealNumber::HaVerCosine().

{
    double a = cos(x);
    double b = 1.0 + a;
    double c = b / 2.0;
    return c;
}

Here is the call graph for this function:

Here is the caller graph for this function:

hypot()

double hypot	(	double	x,
		double	y
	)

hypot

Method
 If (assume round-to-nearest) z=x*x+y*y
 has error less than sqrt(2)/2 ulp, than
 sqrt(z) has error less than 1 ulp (exercise).

 So, compute sqrt(x*x+y*y) with some care as
 follows to get the error below 1 ulp:

 Assume x>y>0;
 (if possible, set rounding to round-to-nearest)
 1. if x > 2y  use
    x1*x1+(y*y+(x2*(x+x1))) for x*x+y*y
 where x1 = x with lower 32 bits cleared, x2 = x-x1; else
 2. if x <= 2y use
    t1*y1+((x-y)*(x-y)+(t1*y2+t2*y))
 where t1 = 2x with lower 32 bits cleared, t2 = 2x-t1,
 y1= y with lower 32 bits chopped, y2 = y-y1.

 NOTE: scaling may be necessary if some argument is too
       large or too tiny

Special cases:
 hypot(x,y) is INF if x or y is +INF or -INF; else
 hypot(x,y) is NAN if x or y is NAN.

Accuracy:
    hypot(x,y) returns sqrt(x^2+y^2) with error less
    than 1 ulps (units in the last place)

Definition at line 81 of file hypot.c.

References sqrt().

Referenced by cabs().

{
    double a = x, b = y, t1, t2, y1, y2, w;
    uint32_t j, k, ha, hb, hx, hy;

    GET_HIGH_WORD(hx, x);
    GET_HIGH_WORD(hy, y);
    ha = hx & 0x7FFFFFFF; // high word of x
    hb = hy & 0x7FFFFFFF; // high word of y

    if (hb > ha)
    {
        a = y;
        b = x;
        j = ha;
        ha = hb;
        hb = j;
    }
    else
    {
        a = x;
        b = y;
    }

    SET_HIGH_WORD(a, ha); // a <- |a|
    SET_HIGH_WORD(b, hb); // b <- |b|

    // x/y > 2**60
    if ((ha - hb) > 0x3C00000)
    {
        return a + b;
    }

    k = 0;

    // a>2**500
    if (ha > 0x5F300000)
    {
        // Inf or NaN
        if (ha >= 0x7FF00000)
        {
            uint32_t la, lb;
            w = a + b; // for sNaN
            GET_LOW_WORD(la, a);
            GET_LOW_WORD(lb, b);

            if (((ha & 0xFFFFF) | la) == 0)
            {
                w = a;
            }

            if (((hb ^ 0x7FF00000) | lb) == 0)
            {
                w = b;
            }

            return w;
        }

        // scale a and b by 2**-600
        ha -= 0x25800000;
        hb -= 0x25800000;
        k += 600;
        SET_HIGH_WORD(a, ha);
        SET_HIGH_WORD(b, hb);
    }

    // b < 2**-500
    if (hb < 0x20B00000)
    {
        // subnormal b or 0
        if (hb <= 0x000FFFFF)
        {
            uint32_t lb;
            GET_LOW_WORD(lb, b);
            if ((hb | lb) == 0)
            {
                return a;
            }

            t1 = 0;
            SET_HIGH_WORD(t1, 0x7FD00000); /* t1=2^1022 */
            b *= t1;
            a *= t1;
            k -= 1022;
        }
        else
        {                     /* scale a and b by 2^600 */
            ha += 0x25800000; /* a *= 2^600 */
            hb += 0x25800000; /* b *= 2^600 */
            k -= 600;

            SET_HIGH_WORD(a, ha);
            SET_HIGH_WORD(b, hb);
        }
    }

    // medium size a and b
    w = a - b;
    if (w > b)
    {
        t1 = 0;
        SET_HIGH_WORD(t1, ha);
        t2 = a - t1;
        w = sqrt(t1 * t1 - (b * (-b) - t2 * (a + t1)));
    }
    else
    {
        a = a + a;
        y1 = 0;
        SET_HIGH_WORD(y1, hb);
        y2 = b - y1;
        t1 = 0;
        SET_HIGH_WORD(t1, ha + 0x00100000);
        t2 = a - t1;
        w = sqrt(t1 * y1 - (w * (-w) - (t1 * y2 + t2 * b)));
    }

    if (k != 0)
    {
        uint32_t ht1;
        t1 = 1.0;
        GET_HIGH_WORD(ht1, t1);
        SET_HIGH_WORD(t1, ht1 + (k << 20));
        return t1 * w;
    }

    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

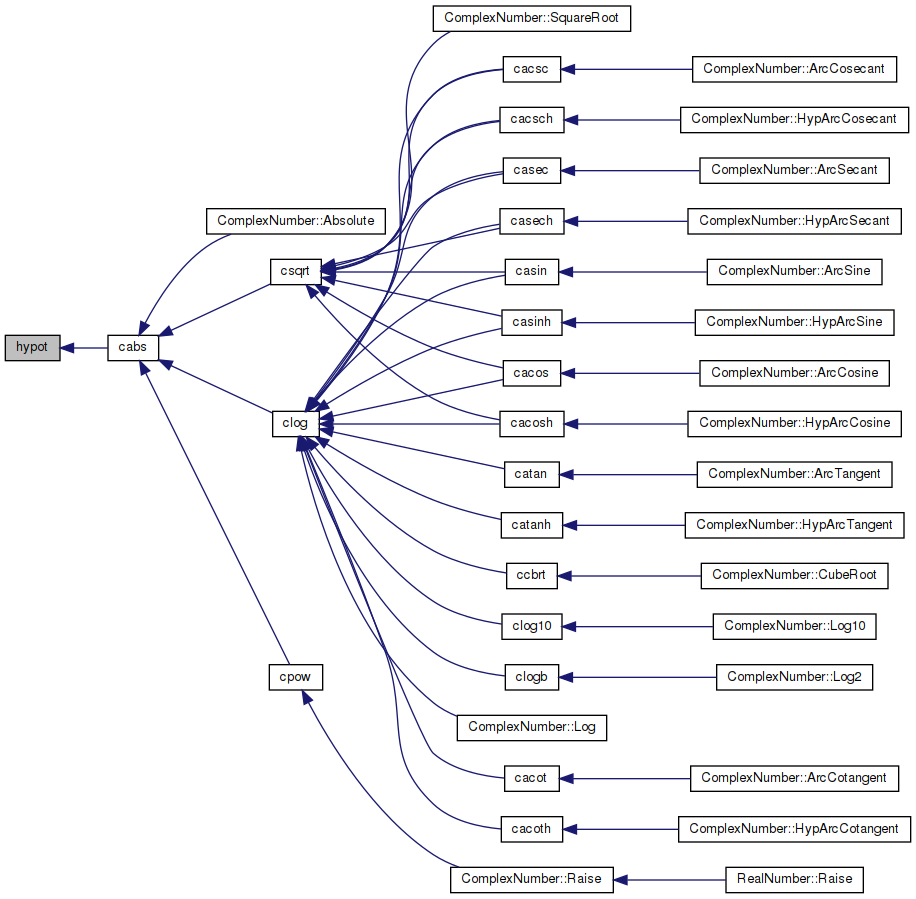
log()

double log

(

double

x

)

Natural logarithm function (base e)

Method
  1. Argument Reduction: find k and f such that
        x = 2^k * (1+f),
    where  sqrt(2)/2 < 1+f < sqrt(2) .

  2. Approximation of log(1+f).
 Let s = f/(2+f) ; based on log(1+f) = log(1+s) - log(1-s)
     = 2s + 2/3 s**3 + 2/5 s**5 + .....,
         = 2s + s*R
     We use a special Remes algorithm on [0,0.1716] to generate
    a polynomial of degree 14 to approximate R The maximum error
 of this polynomial approximation is bounded by 2**-58.45. In
 other words,
            2      4      6      8      10      12      14
     R(z) ~ Lg1*s +Lg2*s +Lg3*s +Lg4*s +Lg5*s  +Lg6*s  +Lg7*s
    (the values of Lg1 to Lg7 are listed in the program)
 and
     |      2          14          |     -58.45
     | Lg1*s +...+Lg7*s    -  R(z) | <= 2
     |                             |
 Note that 2s = f - s*f = f - hfsq + s*hfsq, where hfsq = f*f/2.
 In order to guarantee error in log below 1ulp, we compute log
 by
    log(1+f) = f - s*(f - R)    (if f is not too large)
    log(1+f) = f - (hfsq - s*(hfsq+R)). (better accuracy)

 3. Finally,  log(x) = k*ln2 + log(1+f).
            = k*ln2_hi+(f-(hfsq-(s*(hfsq+R)+k*ln2_lo)))
    Here ln2 is split into two floating point number:
        ln2_hi + ln2_lo,
    where n*ln2_hi is always exact for |n| < 2000.

Special cases:
 log(x) is NaN with signal if x < 0 (including -INF) ;
 log(+INF) is +INF; log(0) is -INF with signal;
 log(NaN) is that NaN with no signal.

Accuracy:
 according to an error analysis, the error is always less than
 1 ulp (unit in the last place).

Constants:
The hexadecimal values are the intended ones for the following
constants. The decimal values may be used, provided that the
compiler will convert from decimal to binary accurately enough
to produce the hexadecimal values shown.

Definition at line 109 of file log.c.

References Lg1, Lg2, Lg3, Lg4, Lg5, Lg6, Lg7, ln2_hi, ln2_lo, two54, and zero.

Referenced by acosh(), acoth(), acsch(), asech(), asinh(), clog(), cpow(), RealNumber::Log(), log10(), RealNumber::Log2(), and log2p().

{
    double hfsq,f,s,z,R,w,t1,t2,dk;
    int32_t k,hx,i,j;
    uint32_t lx;

    EXTRACT_WORDS(hx,lx,x);

    k=0;
    if (hx < 0x00100000) {          /* x < 2**-1022  */
        if (((hx&0x7fffffff)|lx)==0)
            return -two54/zero;     /* log(+-0)=-inf */
        if (hx<0) return (x-x)/zero;    /* log(-#) = NaN */
        k -= 54;
        x *= two54; /* subnormal number, scale up x */
        GET_HIGH_WORD(hx,x);        /* high word of x */
    }
    if (hx >= 0x7ff00000) return x+x;
    k += (hx>>20)-1023;
    hx &= 0x000fffff;
    i = (hx+0x95f64)&0x100000;
    SET_HIGH_WORD(x,hx|(i^0x3ff00000)); /* normalize x or x/2 */
    k += (i>>20);
    f = x-1.0;
    if((0x000fffff&(2+hx))<3) { /* |f| < 2**-20 */
        if(f==zero) {
            if(k==0)
                return zero;
            else {
                dk=(double)k;
                return dk*ln2_hi+dk*ln2_lo;
            }
        }
        R = f*f*(0.5-0.33333333333333333*f);
        if(k==0) return f-R;
        else {
            dk=(double)k;
            return dk*ln2_hi-((R-dk*ln2_lo)-f);
        }
    }
    s = f/(2.0+f);
    dk = (double)k;
    z = s*s;
    i = hx-0x6147a;
    w = z*z;
    j = 0x6b851-hx;
    t1= w*(Lg2+w*(Lg4+w*Lg6));
    t2= z*(Lg1+w*(Lg3+w*(Lg5+w*Lg7)));
    i |= j;
    R = t2+t1;
    if(i>0) {
        hfsq=0.5*f*f;
        if(k==0) return f-(hfsq-s*(hfsq+R));
        else
            return dk*ln2_hi-((hfsq-(s*(hfsq+R)+dk*ln2_lo))-f);
    } else {
        if(k==0) return f-s*(f-R);
        else
            return dk*ln2_hi-((s*(f-R)-dk*ln2_lo)-f);
    }
}

Here is the caller graph for this function:

log10()

double log10

(

double

x

)

Base 10 logarithm function.

Method:
Let log10_2hi = leading 40 bits of log10(2) and
    log10_2lo = log10(2) - log10_2hi,
    ivln10    = 1/log(10) rounded.
Then
    n = ilogb(x),
    if(n<0)  n = n+1;
    x = scalbn(x,-n);
    log10(x) := n*log10_2hi + (n*log10_2lo + ivln10*log(x))

Note 1:
To guarantee log10(10**n)=n, where 10**n is normal, the rounding
mode must set to Round-to-Nearest.

Note 2:
[1/log(10)] rounded to 53 bits has error .198 ulps;
log10 is monotonic at all binary break points.

Special cases:
log10(x) is NaN with signal if x < 0;
log10(+INF) is +INF with no signal; log10(0) is -INF with signal;
log10(NaN) is that NaN with no signal;
log10(10**N) = N  for N=0,1,...,22.

Constants:
The hexadecimal values are the intended ones for the following constants.
The decimal values may be used, provided that the compiler will convert
from decimal to binary accurately enough to produce the hexadecimal values
shown.

Definition at line 93 of file log10.c.

References ivln10, log(), log10_2hi, log10_2lo, two54, and zero.

Referenced by DecimalSystem::GetText(), and RealNumber::Log10().

{
    double y,z;
    int32_t i,k,hx;
    uint32_t lx;

    EXTRACT_WORDS(hx,lx,x);

    k=0;
    if (hx < 0x00100000) {                  /* x < 2**-1022  */
        if (((hx&0x7fffffff)|lx)==0)
            return -two54/zero;             /* log(+-0)=-inf */
        if (hx<0) return (x-x)/zero;        /* log(-#) = NaN */
        k -= 54;
        x *= two54; /* subnormal number, scale up x */
        GET_HIGH_WORD(hx, x);              /* high word of x */
    }
    if (hx >= 0x7ff00000) return x+x;
    k += (hx>>20)-1023;
    i  = ((uint32_t)k&0x80000000)>>31;
    hx = (hx&0x000fffff)|((0x3ff-i)<<20);
    y  = (double)(k+i);
    SET_HIGH_WORD(x,hx);
    z  = y*log10_2lo + ivln10*log(x);
    return  z+y*log10_2hi;
}

Here is the call graph for this function:

Here is the caller graph for this function:

log1p()

double log1p

(

double

x

)

Definition at line 122 of file log1p.c.

References ln2_hi, ln2_lo, Lp1, Lp2, Lp3, Lp4, Lp5, Lp6, Lp7, two54, and zero.

Referenced by acosh(), asinh(), and atanh().

{
    double hfsq,f,c,s,z,R,u;
    int32_t k,hx,hu,ax;

    f = 0.0;
    c = 0.0;
    hu = 0;

    GET_HIGH_WORD(hx,x); /* high word of x */
    ax = hx&0x7fffffff;

    k = 1;
    if (hx < 0x3FDA827A) {          /* x < 0.41422  */
        if(ax>=0x3ff00000) {        /* x <= -1.0 */
            if(x==-1.0) return -two54/zero; /* log1p(-1)=+inf */
            else return (x-x)/(x-x);    /* log1p(x<-1)=NaN */
        }
        if(ax<0x3e200000) {         /* |x| < 2**-29 */
            if(two54+x>zero         /* raise inexact */
                    &&ax<0x3c900000)        /* |x| < 2**-54 */
                return x;
            else
                return x - x*x*0.5;
        }
        if(hx>0||hx<=((int)0xbfd2bec3)) {
            k=0;
            f=x;
            hu=1;
        }   /* -0.2929<x<0.41422 */
    }
    if (hx >= 0x7ff00000) return x+x;
    if(k!=0) {
        if(hx<0x43400000) {
            u  = 1.0+x;
            GET_HIGH_WORD(hu,u); /* high word of u */
            k  = (hu>>20)-1023;
            c  = (k>0)? 1.0-(u-x):x-(u-1.0);/* correction term */
            c /= u;
        } else {
            u  = x;
            GET_HIGH_WORD(hu,u); /* high word of u */
            k  = (hu>>20)-1023;
            c  = 0;
        }
        hu &= 0x000fffff;
        if(hu<0x6a09e) {
            SET_HIGH_WORD(u, hu|0x3ff00000);    /* normalize u */
        } else {
            k += 1;
            SET_HIGH_WORD(u, hu|0x3fe00000);    /* normalize u/2 */
            hu = (0x00100000-hu)>>2;
        }
        f = u-1.0;
    }
    hfsq=0.5*f*f;
    if(hu==0) { /* |f| < 2**-20 */
        if(f==zero) {
            if(k==0) return zero;
            else {
                c += k*ln2_lo;
                return k*ln2_hi+c;
            }
        }
        R = hfsq*(1.0-0.66666666666666666*f);
        if(k==0) return f-R;
        else
            return k*ln2_hi-((R-(k*ln2_lo+c))-f);
    }
    s = f/(2.0+f);
    z = s*s;
    R = z*(Lp1+z*(Lp2+z*(Lp3+z*(Lp4+z*(Lp5+z*(Lp6+z*Lp7))))));
    if(k==0) return f-(hfsq-s*(hfsq+R));
    else
        return k*ln2_hi-((hfsq-(s*(hfsq+R)+(k*ln2_lo+c)))-f);
}

Here is the caller graph for this function:

log2i()

unsigned int log2i

(

unsigned int

x

)

Referenced by Dragon4(), and DecimalSystem::GetText().

Here is the caller graph for this function:

log2p()

double log2p	(	double	x,
		double	y
	)

Definition at line 32 of file log2p.c.

References log().

Referenced by PositionalNumeralSystem::GetText().

{
    return y != 1.0
               ? log(y) / log(x)
               : 0.0;
}

Here is the call graph for this function:

Here is the caller graph for this function:

pow()

double pow	(	double	x,
		double	y
	)

Expontation function.

Method:  Let x =  2   * (1+f)
 1. Compute and return log2(x) in two pieces:
    log2(x) = w1 + w2,
    where w1 has 53-24 = 29 bit trailing zeros.
 2. Perform y*log2(x) = n+y' by simulating muti-precision
    arithmetic, where |y'|<=0.5.
 3. Return x**y = 2**n*exp(y'*log2)

Special cases:
 1.  (anything) ** 0  is 1
 2.  (anything) ** 1  is itself
 3.  (anything) ** NAN is NAN
 4.  NAN ** (anything except 0) is NAN
 5.  +-(|x| > 1) **  +INF is +INF
 6.  +-(|x| > 1) **  -INF is +0
 7.  +-(|x| < 1) **  +INF is +0
 8.  +-(|x| < 1) **  -INF is +INF
 9.  +-1         ** +-INF is NAN
 10. +0 ** (+anything except 0, NAN)               is +0
 11. -0 ** (+anything except 0, NAN, odd integer)  is +0
 12. +0 ** (-anything except 0, NAN)               is +INF
 13. -0 ** (-anything except 0, NAN, odd integer)  is +INF
 14. -0 ** (odd integer) = -( +0 ** (odd integer) )
 15. +INF ** (+anything except 0,NAN) is +INF
 16. +INF ** (-anything except 0,NAN) is +0
 17. -INF ** (anything)  = -0 ** (-anything)
 18. (-anything) ** (integer) is (-1)**(integer)*(+anything**integer)
 19. (-anything except 0 and inf) ** (non-integer) is NAN

Accuracy:
 pow(x,y) returns x**y nearly rounded. In particular
        pow(integer,integer)
 always returns the correct integer provided it is
 representable.

Constants :
The hexadecimal values are the intended ones for the following
constants. The decimal values may be used, provided that the
compiler will convert from decimal to binary accurately enough
to produce the hexadecimal values shown.

Definition at line 138 of file pow.c.

References bp, cp, cp_h, cp_l, dp_h, dp_l, fabs(), huge, ivln2, ivln2_h, ivln2_l, L1, L2, L3, L4, L5, L6, lg2, lg2_h, lg2_l, one, ovt, P1, P2, P3, P4, P5, scalbn(), sqrt(), tiny, two, two53, and zero.

Referenced by cpow(), PositionalNumeralSystem::GetText(), PositionalNumeralSystem::Parse(), and RealNumber::Raise().

{
    double z, ax, z_h, z_l, p_h, p_l;
    double y1, t1, t2, r, s, t, u, v, w;
    int32_t i, j, k, yisint, n;
    int32_t hx, hy, ix, iy;
    uint32_t lx, ly;

    EXTRACT_WORDS(hx, lx, x);
    EXTRACT_WORDS(hy, ly, y);
    ix = hx & 0x7fffffff;
    iy = hy & 0x7fffffff;

    /* y==zero: x**0 = 1 */
    if ((iy | ly) == 0)
        return one;

    /* +-NaN return x+y */
    if (ix > 0x7ff00000 || ((ix == 0x7ff00000) && (lx != 0)) ||
        iy > 0x7ff00000 || ((iy == 0x7ff00000) && (ly != 0)))
        return x + y;

    /* determine if y is an odd int when x < 0
     * yisint = 0   ... y is not an integer
     * yisint = 1   ... y is an odd int
     * yisint = 2   ... y is an even int
     */
    yisint = 0;
    if (hx < 0)
    {
        if (iy >= 0x43400000)
            yisint = 2; /* even integer y */
        else if (iy >= 0x3ff00000)
        {
            k = (iy >> 20) - 0x3ff; /* exponent */
            if (k > 20)
            {
                j = ly >> (52 - k);
                if ((uint32_t)(j << (52 - k)) == ly)
                    yisint = 2 - (j & 1);
            }
            else if (ly == 0)
            {
                j = iy >> (20 - k);
                if ((j << (20 - k)) == iy)
                    yisint = 2 - (j & 1);
            }
        }
    }

    /* special value of y */
    if (ly == 0)
    {
        if (iy == 0x7ff00000)
        { /* y is +-inf */
            if (((ix - 0x3ff00000) | lx) == 0)
                return y - y;          /* inf**+-1 is NaN */
            else if (ix >= 0x3ff00000) /* (|x|>1)**+-inf = inf,0 */
                return (hy >= 0) ? y : zero;
            else /* (|x|<1)**-,+inf = inf,0 */
                return (hy < 0) ? -y : zero;
        }
        if (iy == 0x3ff00000)
        { /* y is  +-1 */
            if (hy < 0)
                return one / x;
            else
                return x;
        }
        if (hy == 0x40000000)
            return x * x; /* y is  2 */
        if (hy == 0x3fe00000)
        {                /* y is  0.5 */
            if (hx >= 0) /* x >= +0 */
                return sqrt(x);
        }
    }

    ax = fabs(x);
    /* special value of x */
    if (lx == 0)
    {
        if (ix == 0x7ff00000 || ix == 0 || ix == 0x3ff00000)
        {
            z = ax; /*x is +-0,+-inf,+-1*/
            if (hy < 0)
                z = one / z; /* z = (1/|x|) */
            if (hx < 0)
            {
                if (((ix - 0x3ff00000) | yisint) == 0)
                {
                    z = (z - z) / (z - z); /* (-1)**non-int is NaN */
                }
                else if (yisint == 1)
                    z = -z; /* (x<0)**odd = -(|x|**odd) */
            }
            return z;
        }
    }

    n = (hx >> 31) + 1;

    /* (x<0)**(non-int) is NaN */
    if ((n | yisint) == 0)
        return (x - x) / (x - x);

    s = one; /* s (sign of result -ve**odd) = -1 else = 1 */
    if ((n | (yisint - 1)) == 0)
        s = -one; /* (-ve)**(odd int) */

    /* |y| is huge */
    if (iy > 0x41e00000)
    { /* if |y| > 2**31 */
        if (iy > 0x43f00000)
        { /* if |y| > 2**64, must o/uflow */
            if (ix <= 0x3fefffff)
                return (hy < 0) ? huge * huge : tiny * tiny;
            if (ix >= 0x3ff00000)
                return (hy > 0) ? huge * huge : tiny * tiny;
        }
        /* over/underflow if x is not close to one */
        if (ix < 0x3fefffff)
            return (hy < 0) ? s * huge * huge : s * tiny * tiny;
        if (ix > 0x3ff00000)
            return (hy > 0) ? s * huge * huge : s * tiny * tiny;
        /* now |1-x| is tiny <= 2**-20, suffice to compute
           log(x) by x-x^2/2+x^3/3-x^4/4 */
        t = ax - one; /* t has 20 trailing zeros */
        w = (t * t) * (0.5 - t * (0.3333333333333333333333 - t * 0.25));
        u = ivln2_h * t; /* ivln2_h has 21 sig. bits */
        v = t * ivln2_l - w * ivln2;
        t1 = u + v;
        SET_LOW_WORD(t1, 0);
        t2 = v - (t1 - u);
    }
    else
    {
        double ss, s2, s_h, s_l, t_h, t_l;
        n = 0;
        /* take care subnormal number */
        if (ix < 0x00100000)
        {
            ax *= two53;
            n -= 53;
            GET_HIGH_WORD(ix, ax);
        }
        n += ((ix) >> 20) - 0x3ff;
        j = ix & 0x000fffff;
        /* determine interval */
        ix = j | 0x3ff00000; /* normalize ix */
        if (j <= 0x3988E)
            k = 0; /* |x|<sqrt(3/2) */
        else if (j < 0xBB67A)
            k = 1; /* |x|<sqrt(3)   */
        else
        {
            k = 0;
            n += 1;
            ix -= 0x00100000;
        }
        SET_HIGH_WORD(ax, ix);

        /* compute ss = s_h+s_l = (x-1)/(x+1) or (x-1.5)/(x+1.5) */
        u = ax - bp[k]; /* bp[0]=1.0, bp[1]=1.5 */
        v = one / (ax + bp[k]);
        ss = u * v;
        s_h = ss;
        SET_LOW_WORD(s_h, 0);
        /* t_h=ax+bp[k] High */
        t_h = zero;
        SET_HIGH_WORD(t_h, ((ix >> 1) | 0x20000000) + 0x00080000 + (k << 18));
        t_l = ax - (t_h - bp[k]);
        s_l = v * ((u - s_h * t_h) - s_h * t_l);
        /* compute log(ax) */
        s2 = ss * ss;
        r = s2 * s2 * (L1 + s2 * (L2 + s2 * (L3 + s2 * (L4 + s2 * (L5 + s2 * L6)))));
        r += s_l * (s_h + ss);
        s2 = s_h * s_h;
        t_h = 3.0 + s2 + r;
        SET_LOW_WORD(t_h, 0);
        t_l = r - ((t_h - 3.0) - s2);
        /* u+v = ss*(1+...) */
        u = s_h * t_h;
        v = s_l * t_h + t_l * ss;
        /* 2/(3log2)*(ss+...) */
        p_h = u + v;
        SET_LOW_WORD(p_h, 0);
        p_l = v - (p_h - u);
        z_h = cp_h * p_h; /* cp_h+cp_l = 2/(3*log2) */
        z_l = cp_l * p_h + p_l * cp + dp_l[k];
        /* log2(ax) = (ss+..)*2/(3*log2) = n + dp_h + z_h + z_l */
        t = (double)n;
        t1 = (((z_h + z_l) + dp_h[k]) + t);
        SET_LOW_WORD(t1, 0);
        t2 = z_l - (((t1 - t) - dp_h[k]) - z_h);
    }

    /* split up y into y1+y2 and compute (y1+y2)*(t1+t2) */
    y1 = y;
    SET_LOW_WORD(y1, 0);
    p_l = (y - y1) * t1 + y * t2;
    p_h = y1 * t1;
    z = p_l + p_h;
    EXTRACT_WORDS(j, i, z);
    if (j >= 0x40900000)
    {                                    /* z >= 1024 */
        if (((j - 0x40900000) | i) != 0) /* if z > 1024 */
            return s * huge * huge;      /* overflow */
        else
        {
            if (p_l + ovt > z - p_h)
                return s * huge * huge; /* overflow */
        }
    }
    else if ((j & 0x7fffffff) >= 0x4090cc00)
    {                                    /* z <= -1075 */
        if (((j - 0xc090cc00) | i) != 0) /* z < -1075 */
            return s * tiny * tiny;      /* underflow */
        else
        {
            if (p_l <= z - p_h)
                return s * tiny * tiny; /* underflow */
        }
    }
    /*
     * compute 2**(p_h+p_l)
     */
    i = j & 0x7fffffff;
    k = (i >> 20) - 0x3ff;
    n = 0;
    if (i > 0x3fe00000)
    { /* if |z| > 0.5, set n = [z+0.5] */
        n = j + (0x00100000 >> (k + 1));
        k = ((n & 0x7fffffff) >> 20) - 0x3ff; /* new k for n */
        t = zero;
        SET_HIGH_WORD(t, (n & ~(0x000fffff >> k)));
        n = ((n & 0x000fffff) | 0x00100000) >> (20 - k);
        if (j < 0)
            n = -n;
        p_h -= t;
    }
    t = p_l + p_h;
    SET_LOW_WORD(t, 0);
    u = t * lg2_h;
    v = (p_l - (t - p_h)) * lg2 + t * lg2_l;
    z = u + v;
    w = v - (z - u);
    t = z * z;
    t1 = z - t * (P1 + t * (P2 + t * (P3 + t * (P4 + t * P5))));
    r = (z * t1) / (t1 - two) - (w + z * w);
    z = one - (r - z);
    GET_HIGH_WORD(j, z);
    j += (n << 20);
    if ((j >> 20) <= 0)
        z = scalbn(z, n); /* subnormal output */
    else
    {
        uint32_t hz;
        GET_HIGH_WORD(hz, z);
        SET_HIGH_WORD(z, hz + (n << 20));
    }
    return s * z;
}

Here is the call graph for this function:

Here is the caller graph for this function:

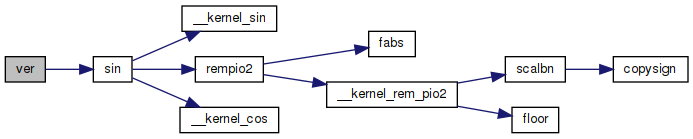
rempio2()

int rempio2	(	double	x,
		double *	y
	)

Definition at line 104 of file remp2.c.

References __kernel_rem_pio2(), fabs(), half, invpio2, npio2_hw, pio2_1, pio2_1t, pio2_2, pio2_2t, pio2_3, pio2_3t, two24, two_over_pi, and zero.

Referenced by cos(), sin(), and tan().

{
    double z = 0.,w,t,r,fn;
    double tx[3];
    int32_t i,j,n,ix,hx;
    int e0,nx;
    uint32_t low;

    GET_HIGH_WORD(hx,x);        /* high word of x */
    ix = hx&0x7fffffff;
    if(ix<=0x3fe921fb)   /* |x| ~<= pi/4 , no need for reduction */
    {
        y[0] = x;
        y[1] = 0;
        return 0;
    }
    if(ix<0x4002d97c) {  /* |x| < 3pi/4, special case with n=+-1 */
        if(hx>0) {
            z = x - pio2_1;
            if(ix!=0x3ff921fb) {    /* 33+53 bit pi is good enough */
                y[0] = z - pio2_1t;
                y[1] = (z-y[0])-pio2_1t;
            } else {        /* near pi/2, use 33+33+53 bit pi */
                z -= pio2_2;
                y[0] = z - pio2_2t;
                y[1] = (z-y[0])-pio2_2t;
            }
            return 1;
        } else {    /* negative x */
            z = x + pio2_1;
            if(ix!=0x3ff921fb) {    /* 33+53 bit pi is good enough */
                y[0] = z + pio2_1t;
                y[1] = (z-y[0])+pio2_1t;
            } else {        /* near pi/2, use 33+33+53 bit pi */
                z += pio2_2;
                y[0] = z + pio2_2t;
                y[1] = (z-y[0])+pio2_2t;
            }
            return -1;
        }
    }
    if(ix<=0x413921fb) { /* |x| ~<= 2^19*(pi/2), medium size */
        t  = fabs(x);
        n  = (int32_t) (t*invpio2+half);
        fn = (double)n;
        r  = t-fn*pio2_1;
        w  = fn*pio2_1t;    /* 1st round good to 85 bit */
        if(n<32&&ix!=npio2_hw[n-1]) {
            y[0] = r-w; /* quick check no cancellation */
        } else {
            uint32_t high;

            j  = ix>>20;
            y[0] = r-w;
            GET_HIGH_WORD(high, y[0]);
            i = j-((high>>20)&0x7ff);
            if(i>16) {  /* 2nd iteration needed, good to 118 */
                t  = r;
                w  = fn*pio2_2;
                r  = t-w;
                w  = fn*pio2_2t-((t-r)-w);
                y[0] = r-w;
                GET_HIGH_WORD(high,y[0]);
                i = j-((high>>20)&0x7ff);
                if(i>49)  { /* 3rd iteration need, 151 bits acc */
                    t  = r; /* will cover all possible cases */
                    w  = fn*pio2_3;
                    r  = t-w;
                    w  = fn*pio2_3t-((t-r)-w);
                    y[0] = r-w;
                }
            }
        }
        y[1] = (r-y[0])-w;
        if(hx<0)    {
            y[0] = -y[0];
            y[1] = -y[1];
            return -n;
        }
        else     return n;
    }
    /*
     * all other (large) arguments
     */
    if(ix>=0x7ff00000) {        /* x is inf or NaN */
        y[0]=y[1]=x-x;
        return 0;
    }
    /* set z = scalbn(|x|,ilogb(x)-23) */
    GET_LOW_WORD(low,x);
    SET_LOW_WORD(z,low);
    e0  = (int32_t)(ix>>20)-1046;   /* e0 = ilogb(z)-23; */
    SET_HIGH_WORD(z,ix - (e0<<20));
    for(i=0; i<2; i++) {
        tx[i] = (double)((int32_t)(z));
        z     = (z-tx[i])*two24;
    }
    tx[2] = z;
    nx = 3;
    while(tx[nx-1]==zero) nx--; /* skip zero term */
    n  =  __kernel_rem_pio2(tx,y,e0,nx,2,two_over_pi);
    if(hx<0) {
        y[0] = -y[0];
        y[1] = -y[1];
        return -n;
    }
    return n;
}

Here is the call graph for this function:

Here is the caller graph for this function:

round()

double round

(

double

x

)

Round function.

Definition at line 40 of file round.c.

References ceil(), and floor().

Referenced by cround(), PositionalNumeralSystem::GetText(), and RealNumber::Round().

{
    return x > 0.0
               ? floor(x + 0.5)
               : ceil(x - 0.5);
}

Here is the call graph for this function:

Here is the caller graph for this function:

scalbn()

double scalbn	(	double	x,
		int	n
	)

sec()

double sec

(

double

x

)

Secant function.

sec(x) = 1/cos(x)
       = 1/sqrt(cos(x)*cos(x))

Definition at line 45 of file sec.c.

References cos(), and sqrt().

Referenced by exs(), and RealNumber::Secant().

{
    double a, b, c;

    a = cos(x);
    if (a == 0.0)
    {
        return NAN;
    }

    b = sqrt(a * a);
    c = 1.0 / b;

    return c;
}

Here is the call graph for this function:

Here is the caller graph for this function:

sech()

double sech

(

double

x

)

Hyperbolic secant function.

sech(x) = 1/cosh(x)

Definition at line 44 of file sech.c.

References cosh().

Referenced by RealNumber::HypSecant().

{
    double a = cosh(x);
    if (TRIG_INEXACT(a))
    {
        return NAN;
    }
    return 1.0 / a;
}

Here is the call graph for this function:

Here is the caller graph for this function:

sin()

double sin

(

double

x

)

Sine function.

Returns

Sine function of x

Kernel function:
__kernel_sin        ... sine function on [-pi/4,pi/4]
__kernel_cos        ... cose function on [-pi/4,pi/4]
__ieee754_rem_pio2  ... argument reduction routine

Method:
Let S,C and T denote the sin, cos and tan respectively on
[-PI/4, +PI/4]. Reduce the argument x to y1+y2 = x-k*pi/2
in [-pi/4 , +pi/4], and let n = k mod 4.

We have

     n        sin(x)      cos(x)        tan(x)
----------------------------------------------------------
     0          S           C             T
     1          C          -S           -1/T
     2         -S          -C             T
     3         -C           S           -1/T
----------------------------------------------------------

Special cases:
Let trig be any of sin, cos, or tan.
trig(+-INF)  is NaN
trig(NaN)    is that NaN

Accuracy:
TRIG(x) returns trig(x) nearly rounded

Definition at line 86 of file sin.c.

References __kernel_cos(), __kernel_sin(), and rempio2().

Referenced by ccos(), ccosh(), ccot(), ccoth(), ccsc(), ccsch(), cexp(), cot(), cpow(), crd(), csc(), csec(), csech(), csin(), csinh(), ctan(), ctanh(), cvc(), cvs(), hcc(), hcv(), RealNumber::Sine(), and ver().

{
    double y[2], z = 0.0;
    int32_t n, ix;

    GET_HIGH_WORD(ix, x);
    ix &= 0x7FFFFFFF;

    // |x| ~< pi/4
    if (ix <= 0x3FE921FB)
    {
        return __kernel_sin(x, z, 0);
    }

    // sin(Inf or NaN) is NaN
    if (ix >= 0x7FF00000)
    {
        return NAN;
    }

    // argument reduction needed
    n = rempio2(x, y);
    switch (n & 3)
    {
    case 0:
        return __kernel_sin(y[0], y[1], 1);
    case 1:
        return __kernel_cos(y[0], y[1]);
    case 2:
        return -__kernel_sin(y[0], y[1], 1);
    default:
        return -__kernel_cos(y[0], y[1]);
    }
}

Here is the call graph for this function:

Here is the caller graph for this function:

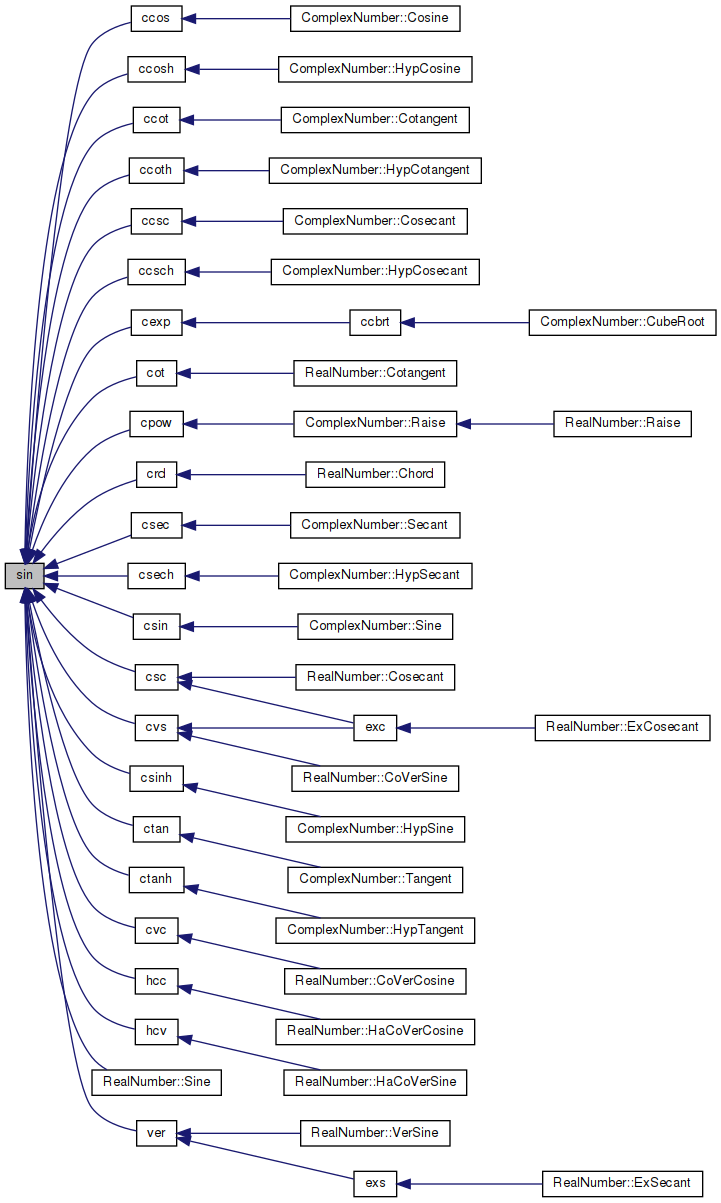
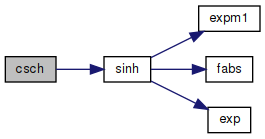
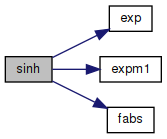
sinh()

double sinh

(

double

x

)

Hyperbolic sine function.

Method
mathematically sinh(x) if defined to be (exp(x)-exp(-x))/2
 1. Replace x by |x| (sinh(-x) = -sinh(x)).
 2.
                                        E + E/(E+1)
     0        <= x <= 22     :  sinh(x) := -----------—, E=expm1(x)
                                2

     22       <= x <= lnovft :  sinh(x) := exp(x)/2
     lnovft   <= x <= ln2ovft:  sinh(x) := exp(x/2)/2 * exp(x/2)
     ln2ovft  <  x      :  sinh(x) := x*shuge (overflow)

Special cases
    sinh(x) is |x| if x is +INF, -INF, or NaN.
    only sinh(0)=0 is exact for finite x.

Definition at line 77 of file sinh.c.

References exp(), expm1(), fabs(), one, and shuge.

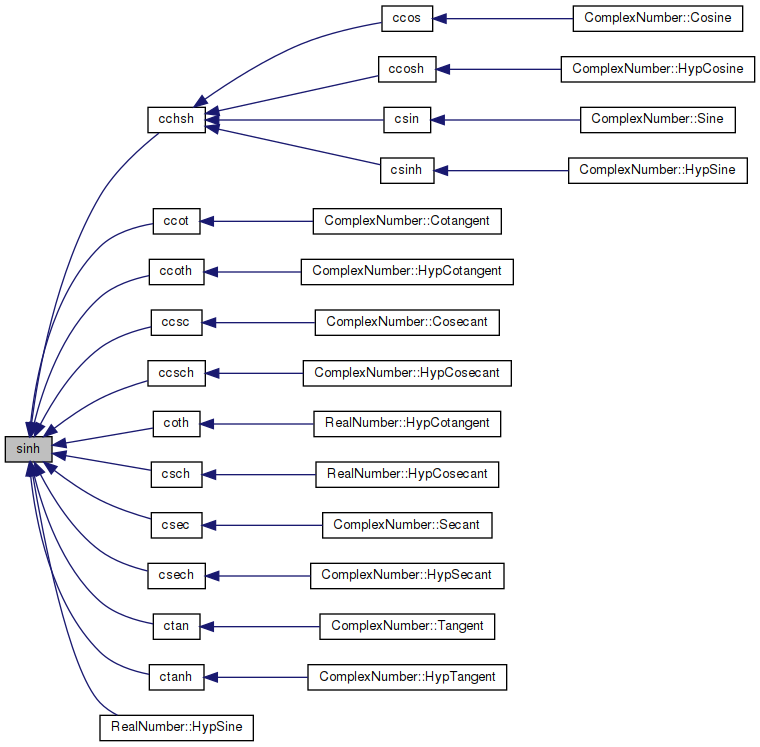
Referenced by cchsh(), ccot(), ccoth(), ccsc(), ccsch(), coth(), csch(), csec(), csech(), ctan(), ctanh(), and RealNumber::HypSine().

{
    double t, w, h;
    int32_t ix, jx;
    uint32_t lx;

    // High word of |x|
    GET_HIGH_WORD(jx, x);
    ix = jx & 0x7FFFFFFF;

    // x is INF or NaN
    if (ix >= 0x7FF00000)
    {
        return NAN;
    }

    h = 0.5;
    if (jx < 0)
        h = -h;
    /* |x| in [0,22], return sign(x)*0.5*(E+E/(E+1))) */
    if (ix < 0x40360000)
    {                        /* |x|<22 */
        if (ix < 0x3E300000) /* |x|<2**-28 */
            if (shuge + x > one)
                return x; /* sinh(tiny) = tiny with inexact */
        t = expm1(fabs(x));
        if (ix < 0x3FF00000)
            return h * (2.0 * t - t * t / (t + one));
        return h * (t + t / (t + one));
    }

    /* |x| in [22, log(maxdouble)] return 0.5*exp(|x|) */
    if (ix < 0x40862E42)
        return h * exp(fabs(x));

    /* |x| in [log(maxdouble), overflowthresold] */
    lx = *((((*(uint32_t *)&one) >> 29)) + (uint32_t *)&x);
    if (ix < 0x408633CE || ((ix == 0x408633CE) && (lx <= (uint32_t)0X8FB9F87D)))
    {
        w = exp(0.5 * fabs(x));
        t = h * w;
        return t * w;
    }

    /* |x| > overflowthresold, sinh(x) overflow */
    return x * shuge;
}

Here is the call graph for this function:

Here is the caller graph for this function:

sqrt()

double sqrt

(

double

x

)

Square root function.

Returns

Correctly rounded sqrt

Method:
  Bit by bit method using integer arithmetic. (Slow, but portable)
  1. Normalization
     Scale x to y in [1,4) with even powers of 2:
     find an integer k such that  1 <= (y=x*2^(2k)) < 4, then
     sqrt(x) = 2^k * sqrt(y)
  2. Bit by bit computation
     Let q  = sqrt(y) truncated to i bit after binary point (q = 1),
          i                          0
                                    i+1         2
         s  = 2*q , and y  =  2   * ( y - q  ).     (1)
          i      i            i                 i

     To compute q    from q , one checks whether
        i+1       i
  -(i+1) 2

        (q + 2      ) <= y.         (2)
                  i
                              -(i+1)
 If (2) is false, then q   = q ; otherwise q   = q  + 2      .
               i+1   i             i+1   i

     With some algebric manipulation, it is not difficult to see
     that (2) is equivalent to
                            -(i+1)
        s  +  2       <= y          (3)
         i                i

     The advantage of (3) is that s  and y  can be computed by
                  i      i
     the following recurrence formula:
         if (3) is false

         s     =  s  ,  y    = y   ;            (4)
          i+1      i         i+1    i

         otherwise,
                        -i                     -(i+1)
         s    =  s  + 2  ,  y    = y  -  s  - 2         (5)
          i+1      i          i+1    i     i

     One may easily use induction to prove (4) and (5).
     Note. Since the left hand side of (3) contain only i+2 bits,
         it does not necessary to do a full (53-bit) comparison
         in (3).
  3. Final rounding
     After generating the 53 bits result, we compute one more bit.
     Together with the remainder, we can decide whether the
     result is exact, bigger than 1/2ulp, or less than 1/2ulp
     (it will never equal to 1/2ulp).
     The rounding mode can be detected by checking whether
     huge + tiny is equal to huge, and whether huge - tiny is
     equal to huge for some floating point number "huge" and "tiny".

Special cases:
  sqrt(+-0) = +-0    ... exact
  sqrt(inf) = inf
  sqrt(-ve) = NaN    ... with invalid signal
  sqrt(NaN) = NaN    ... with invalid signal for signaling NaN

Definition at line 119 of file sqrt.c.

References one, and tiny.

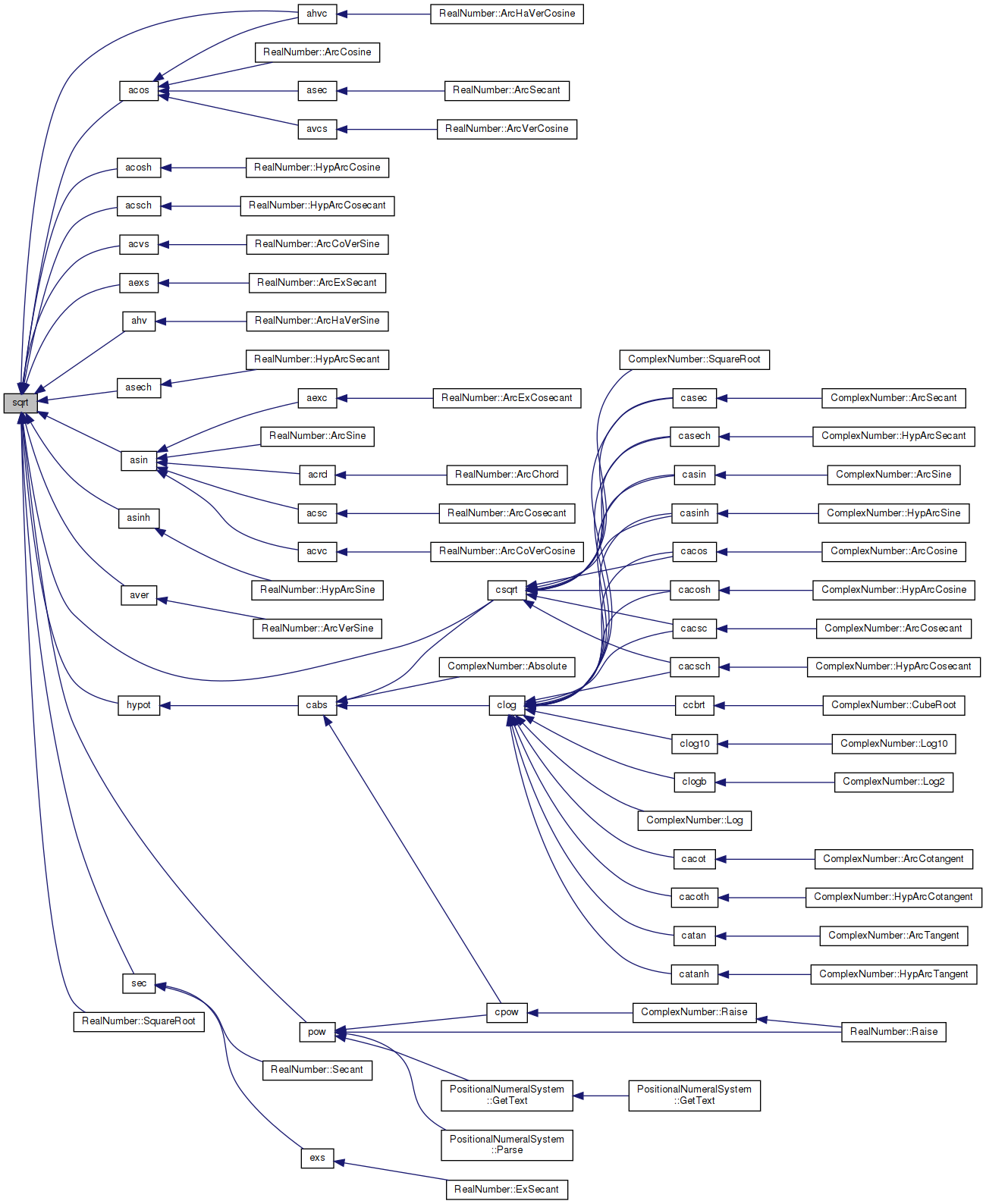
Referenced by acos(), acosh(), acsch(), acvs(), aexs(), ahv(), ahvc(), asech(), asin(), asinh(), aver(), csqrt(), hypot(), pow(), sec(), and RealNumber::SquareRoot().

{
    double z;
    int32_t sign = (int32_t)0x80000000;
    uint32_t r, t1, s1, ix1, q1;
    int32_t ix0, s0, q, m, t, i;

    EXTRACT_WORDS(ix0, ix1, x);

    // take care of Inf and NaN
    if ((ix0 & 0x7FF00000) == 0x7FF00000)
    {
        // sqrt(NaN)=NaN
        // sqrt(+inf)=+inf
        // sqrt(-inf)=sNaN
        return x * x + x;
    }

    // take care of zero
    if (ix0 <= 0)
    {
        if (((ix0 & (~sign)) | ix1) == 0)
        {
            // sqrt(+-0) = +-0
            return x;
        }
        else if (ix0 < 0)
        {
            //sqrt(-ve) = NaN
            return NAN;
        }
    }

    // normalize x
    m = (ix0 >> 20);
    if (m == 0)
    {
        // subnormal x
        while (ix0 == 0)
        {
            m -= 21;
            ix0 |= (ix1 >> 11);
            ix1 <<= 21;
        }

        for (i = 0; (ix0 & 0x00100000) == 0; i++)
        {
            ix0 <<= 1;
        }

        m -= i - 1;
        ix0 |= (ix1 >> (32 - i));
        ix1 <<= i;
    }

    m -= 1023; // unbias exponent
    ix0 = (ix0 & 0x000FFFFF) | 0x00100000;
    if (m & 1)
    {
        // odd m, double x to make it even
        ix0 += ix0 + ((ix1 & sign) >> 31);
        ix1 += ix1;
    }

    // m = [m/2]
    m >>= 1;

    // generate sqrt(x) bit by bit
    ix0 += ix0 + ((ix1 & sign) >> 31);
    ix1 += ix1;
    q = q1 = s0 = s1 = 0; // [q,q1] = sqrt(x)
    r = 0x00200000;       // r = moving bit from right to left

    while (r != 0)
    {
        t = s0 + r;
        if (t <= ix0)
        {
            s0 = t + r;
            ix0 -= t;
            q += r;
        }
        ix0 += ix0 + ((ix1 & sign) >> 31);
        ix1 += ix1;
        r >>= 1;
    }

    r = sign;
    while (r != 0)
    {
        t1 = s1 + r;
        t = s0;
        if ((t < ix0) || ((t == ix0) && (t1 <= ix1)))
        {
            s1 = t1 + r;
            if (((t1 & sign) == (uint32_t)sign) && (s1 & sign) == 0)
            {
                s0 += 1;
            }
            ix0 -= t;
            if (ix1 < t1)
            {
                ix0 -= 1;
            }
            ix1 -= t1;
            q1 += r;
        }

        ix0 += ix0 + ((ix1 & sign) >> 31);
        ix1 += ix1;
        r >>= 1;
    }

    // use floating add to find out rounding direction
    if ((ix0 | ix1) != 0)
    {
        // trigger inexact flag
        z = one - tiny;
        if (z >= one)
        {
            z = one + tiny;
            if (q1 == (uint32_t)0xFFFFFFFF)
            {
                q1 = 0;
                q += 1;
            }
            else if (z > one)
            {
                if (q1 == (uint32_t)0xFFFFFFFE)
                {
                    q += 1;
                }
                q1 += 2;
            }
            else
            {
                q1 += (q1 & 1);
            }
        }
    }

    ix0 = (q >> 1) + 0x3FE00000;
    ix1 = q1 >> 1;
    if ((q & 1) == 1)
    {
        ix1 |= sign;
    }

    ix0 += (m << 20);
    INSERT_WORDS(z, ix0, ix1);

    return z;
}

Here is the caller graph for this function:

tan()

double tan

(

double

x

)

Tangent function.

Returns

Tangent function of x

Kernel function:
__kernel_sin        ... sine function on [-pi/4,pi/4]
__kernel_cos        ... cose function on [-pi/4,pi/4]
__ieee754_rem_pio2  ... argument reduction routine

Method:
Let S,C and T denote the sin, cos and tan respectively on
[-PI/4, +PI/4]. Reduce the argument x to y1+y2 = x-k*pi/2
in [-pi/4 , +pi/4], and let n = k mod 4.

We have

     n        sin(x)      cos(x)        tan(x)
----------------------------------------------------------
     0          S           C             T
     1          C          -S           -1/T
     2         -S          -C             T
     3         -C           S           -1/T
----------------------------------------------------------

Special cases:
Let trig be any of sin, cos, or tan.
trig(+-INF)  is NaN
trig(NaN)    is that NaN

Accuracy:
TRIG(x) returns trig(x) nearly rounded

Definition at line 87 of file tan.c.

References __kernel_tan(), and rempio2().

Referenced by RealNumber::Tangent().

{
    double y[2], z = 0.0;
    int32_t n, ix;

    GET_HIGH_WORD(ix, x);
    ix &= 0x7FFFFFFF;

    // |x| ~< pi/4
    if (ix <= 0x3FE921FB)
    {
        return __kernel_tan(x, z, 1);
    }

    // tan(Inf or NaN) is NaN
    if (ix >= 0x7FF00000)
    {
        return NAN;
    }

    // |x| ~< pi/4
    n = rempio2(x, y);
    return __kernel_tan(y[0], y[1], 1 - ((n & 1) << 1));
}

Here is the call graph for this function:

Here is the caller graph for this function:

tanh()

double tanh

(

double

x

)

Hyperbolic tangent function.

Returns

The Hyperbolic Tangent of x

Method
                                   x    -x
                                  e  - e
    0. tanh(x) is defined to be --------—
                                   x    -x
                                  e  + e

    1. reduce x to non-negative by tanh(-x) = -tanh(x)

    2.  0      <= x <= 2**-55 : tanh(x) = x*(one+x)
                                           -t
        2**-55 <  x <=  1     : tanh(x) = --—; t = expm1(-2x)
                                          t + 2
                                                2
        1      <= x <=  22.0  : tanh(x) = 1-  --— ; t=expm1(2x)
                                              t + 2
        22.0   <  x <= INF    : tanh(x) = 1

Special cases
    tanh(NaN) is NaN
    only tanh(0)=0 is exact for finite argument.

Definition at line 81 of file tanh.c.

References expm1(), fabs(), one, tiny, and two.

Referenced by RealNumber::HypTangent().

{
    double t, z;
    int32_t jx, ix;

    /* High word of |x|. */
    GET_HIGH_WORD(jx, x);
    ix = jx & 0x7FFFFFFF;

    /* x is INF or NaN */
    if (ix >= 0x7FF00000)
    {
        if (jx >= 0)
            return one / x + one; /* tanh(+-inf)=+-1 */
        else
            return NAN; /* tanh(NaN) = NaN */
    }

    /* |x| < 22 */
    if (ix < 0x40360000)
    {                             /* |x|<22 */
        if (ix < 0x3C800000)      /* |x|<2**-55 */
            return x * (one + x); /* tanh(small) = small */
        if (ix >= 0x3FF00000)
        { /* |x|>=1 */
            t = expm1(two * fabs(x));
            z = one - two / (t + two);
        }
        else
        {
            t = expm1(-two * fabs(x));
            z = -t / (t + two);
        }
    }
    /* |x| > 22, return +-1 */
    else
    {
        z = one - tiny; /* raised inexact flag */
    }

    return (jx >= 0) ? z : -z;
}

Here is the call graph for this function:

Here is the caller graph for this function:

trunc()

double trunc

(

double

x

)

Truncate function.

when x > 0
trunc(0)   = floor(x)

when x < 0
trunc(x)   = ceil(x)

Special case
trunc(0)   = 0
trunc(NaN) = NaN

Definition at line 52 of file trunc.c.

References ceil(), and floor().

Referenced by ctrunc(), DecimalSystem::GetText(), PositionalNumeralSystem::GetText(), PositionalNumeralSystem::IntegerToBuffer(), and RealNumber::Trunc().

{
    uint32_t hx, lx;
    GET_HIGH_WORD(hx, x);
    if ((hx & 0x7FF00000) == 0x7FF00000)
    {
        return NAN;
    }

    GET_LOW_WORD(lx, x);
    if (hx == 0 && lx == 0)
    {
        return 0.0;
    }

    if ((hx & 0x80000000) != 0x80000000)
    {
        return floor(x);
    }

    return ceil(x);
}

Here is the call graph for this function:

Here is the caller graph for this function:

vcs()

double vcs

(

double

x

)

Versed cosine function.

vercos = 1+cos(x)
       = 2*cos(x/2)*cos(x/2)

Definition at line 45 of file vcs.c.

References cos().

Referenced by RealNumber::VerCosine().

{
    double a = x / 2.0;
    double b = cos(a);
    double c = 2 * b * b;
    return c;
}

Here is the call graph for this function:

Here is the caller graph for this function:

ver()

double ver

(

double

x

)

Versed sine function.

versin = 1-cos(x)
       = 2*sin(x/2)*sin(x/2)

Definition at line 45 of file ver.c.

References sin().

Referenced by exs(), and RealNumber::VerSine().

{
    double a = x / 2.0;
    double b = sin(a);
    double c = 2 * b * b;
    return c;
}

Here is the call graph for this function:

Here is the caller graph for this function: