Hyperbolic sine function. More...

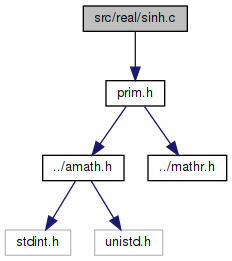
#include "prim.h"

Include dependency graph for sinh.c:

Functions
double	sinh (double x)
	Hyperbolic sine function. More...

Variables
static const double	one = 1.0

static const double	shuge = 1.0e307

Detailed Description

Hyperbolic sine function.

Definition in file sinh.c.

Function Documentation

◆ sinh()

double sinh ( double x )

Hyperbolic sine function.

Method
mathematically sinh(x) if defined to be (exp(x)-exp(-x))/2
 1. Replace x by |x| (sinh(-x) = -sinh(x)).
 2.
                                        E + E/(E+1)
     0        <= x <= 22     :  sinh(x) := -----------—, E=expm1(x)
                                2

     22       <= x <= lnovft :  sinh(x) := exp(x)/2
     lnovft   <= x <= ln2ovft:  sinh(x) := exp(x/2)/2 * exp(x/2)
     ln2ovft  <  x      :  sinh(x) := x*shuge (overflow)

Special cases
    sinh(x) is |x| if x is +INF, -INF, or NaN.
    only sinh(0)=0 is exact for finite x.

Definition at line 77 of file sinh.c.

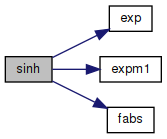
References exp(), expm1(), fabs(), one, and shuge.

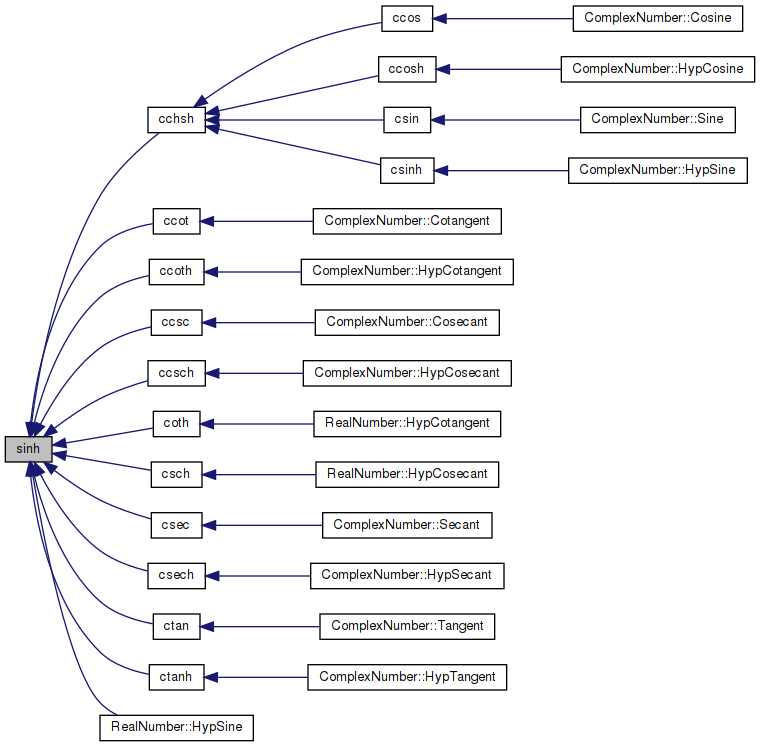
Referenced by cchsh(), ccot(), ccoth(), ccsc(), ccsch(), coth(), csch(), csec(), csech(), ctan(), ctanh(), and RealNumber::HypSine().

 {
     double t, w, h;
     int32_t ix, jx;
     uint32_t lx;
 
     // High word of |x|
     GET_HIGH_WORD(jx, x);
     ix = jx & 0x7FFFFFFF;
 
     // x is INF or NaN
     if (ix >= 0x7FF00000)
     {
         return NAN;
     }
 
     h = 0.5;
     if (jx < 0)
         h = -h;
     /* |x| in [0,22], return sign(x)*0.5*(E+E/(E+1))) */
     if (ix < 0x40360000)
     {                        /* |x|<22 */
         if (ix < 0x3E300000) /* |x|<2**-28 */
             if (shuge + x > one)
                 return x; /* sinh(tiny) = tiny with inexact */
         t = expm1(fabs(x));
         if (ix < 0x3FF00000)
             return h * (2.0 * t - t * t / (t + one));
         return h * (t + t / (t + one));
     }
 
     /* |x| in [22, log(maxdouble)] return 0.5*exp(|x|) */
     if (ix < 0x40862E42)
         return h * exp(fabs(x));
 
     /* |x| in [log(maxdouble), overflowthresold] */
     lx = *((((*(uint32_t *)&one) >> 29)) + (uint32_t *)&x);
     if (ix < 0x408633CE || ((ix == 0x408633CE) && (lx <= (uint32_t)0X8FB9F87D)))
     {
         w = exp(0.5 * fabs(x));
         t = h * w;
         return t * w;
     }
 
     /* |x| > overflowthresold, sinh(x) overflow */
     return x * shuge;
 }

Here is the call graph for this function:

Here is the caller graph for this function:

Variable Documentation

◆ one

const double one = 1.0

static

Definition at line 53 of file sinh.c.

Referenced by sinh().

◆ shuge

const double shuge = 1.0e307