Primitives in math library for handling real numbers. More...
Include dependency graph for prim.h:
This graph shows which files directly or indirectly include this file:
Go to the source code of this file.
Macros | |
| #define | TRIG_INEXACT(x) ((x >= 0.0 && x < 1e-15) || (x <= 0.0 && x > -1e-15)) |
| #define | EXTRACT_WORDS(ix0, ix1, d) |
| Get two 32 bit ints from a double. More... | |
| #define | GET_HIGH_WORD(i, d) |
| Get the more significant 32 bit int from a double. More... | |
| #define | GET_LOW_WORD(i, d) |
| Get the less significant 32 bit int from a double. More... | |
| #define | INSERT_WORDS(d, ix0, ix1) |
| Set a double from two 32 bit ints. More... | |
| #define | SET_HIGH_WORD(d, v) |
| Set the more significant 32 bits of a double from an int. More... | |
| #define | SET_LOW_WORD(d, v) |
| Set the less significant 32 bits of a double from an int. More... | |
Functions | |
| double | __kernel_cos (double x, double y) |
| Kernel cosine function. More... | |
| double | __kernel_sin (double x, double y, int iy) |
| Kernel sin function. More... | |
| double | __kernel_tan (double x, double y, int iy) |
| Kernel tan function. More... | |
| int | __kernel_rem_pio2 (double *x, double *y, int e0, int nx, int prec, const int *ipio2) |
| Kernel reduction function. More... | |
Detailed Description
Primitives in math library for handling real numbers.
The library is based on fdlib by Sun Microsystems. The original library can be downloaded at: http://www.netlib.org/fdlibm/
or from mirror site: http://www.hensa.ac.uk/
Definition in file prim.h.
Macro Definition Documentation
◆ EXTRACT_WORDS
| #define EXTRACT_WORDS | ( | ix0, | |
| ix1, | |||
| d | |||
| ) |
◆ GET_HIGH_WORD
| #define GET_HIGH_WORD | ( | i, | |
| d | |||
| ) |
◆ GET_LOW_WORD
| #define GET_LOW_WORD | ( | i, | |
| d | |||
| ) |
◆ INSERT_WORDS
| #define INSERT_WORDS | ( | d, | |
| ix0, | |||
| ix1 | |||
| ) |
◆ SET_HIGH_WORD
| #define SET_HIGH_WORD | ( | d, | |
| v | |||
| ) |
◆ SET_LOW_WORD
| #define SET_LOW_WORD | ( | d, | |
| v | |||
| ) |
◆ TRIG_INEXACT
| #define TRIG_INEXACT | ( | x | ) | ((x >= 0.0 && x < 1e-15) || (x <= 0.0 && x > -1e-15)) |
Function Documentation
◆ __kernel_cos()
| double __kernel_cos | ( | double | x, |
| double | y | ||
| ) |
Kernel cosine function.
Kernel cos function on [-pi/4, pi/4], pi/4 ~ 0.785398164 Input x is assumed to be bounded by ~pi/4 in magnitude. Input y is the tail of x.
Algorithm
1. Since cos(-x) = cos(x), we need only to consider positive x.
2. if x < 2^-27 (hx<0x3e400000 0), return 1 with inexact if x!=0.
3. cos(x) is approximated by a polynomial of degree 14 on
[0,pi/4]
4 14
cos(x) ~ 1 - x*x/2 + C1*x + ... + C6*x
where the Remes error is | 2 4 6 8 10 12 14 | -58
|cos(x)-(1-.5*x +C1*x +C2*x +C3*x +C4*x +C5*x +C6*x )| <= 2
| |
4 6 8 10 12 14
4. let r = C1*x +C2*x +C3*x +C4*x +C5*x +C6*x , then
cos(x) = 1 - x*x/2 + r
since cos(x+y) ~ cos(x) - sin(x)*y
~ cos(x) - x*y,
a correction term is necessary in cos(x) and hence
cos(x+y) = 1 - (x*x/2 - (r - x*y))
For better accuracy when x > 0.3, let qx = |x|/4 with
the last 32 bits mask off, and if x > 0.78125, let qx = 0.28125.
Then
cos(x+y) = (1-qx) - ((x*x/2-qx) - (r-x*y)).
Note that 1-qx and (x*x/2-qx) is EXACT here, and the
magnitude of the latter is at least a quarter of x*x/2,
thus, reducing the rounding error in the subtraction.
Definition at line 94 of file kcos.c.
References C1, C2, C3, C4, C5, C6, and one.
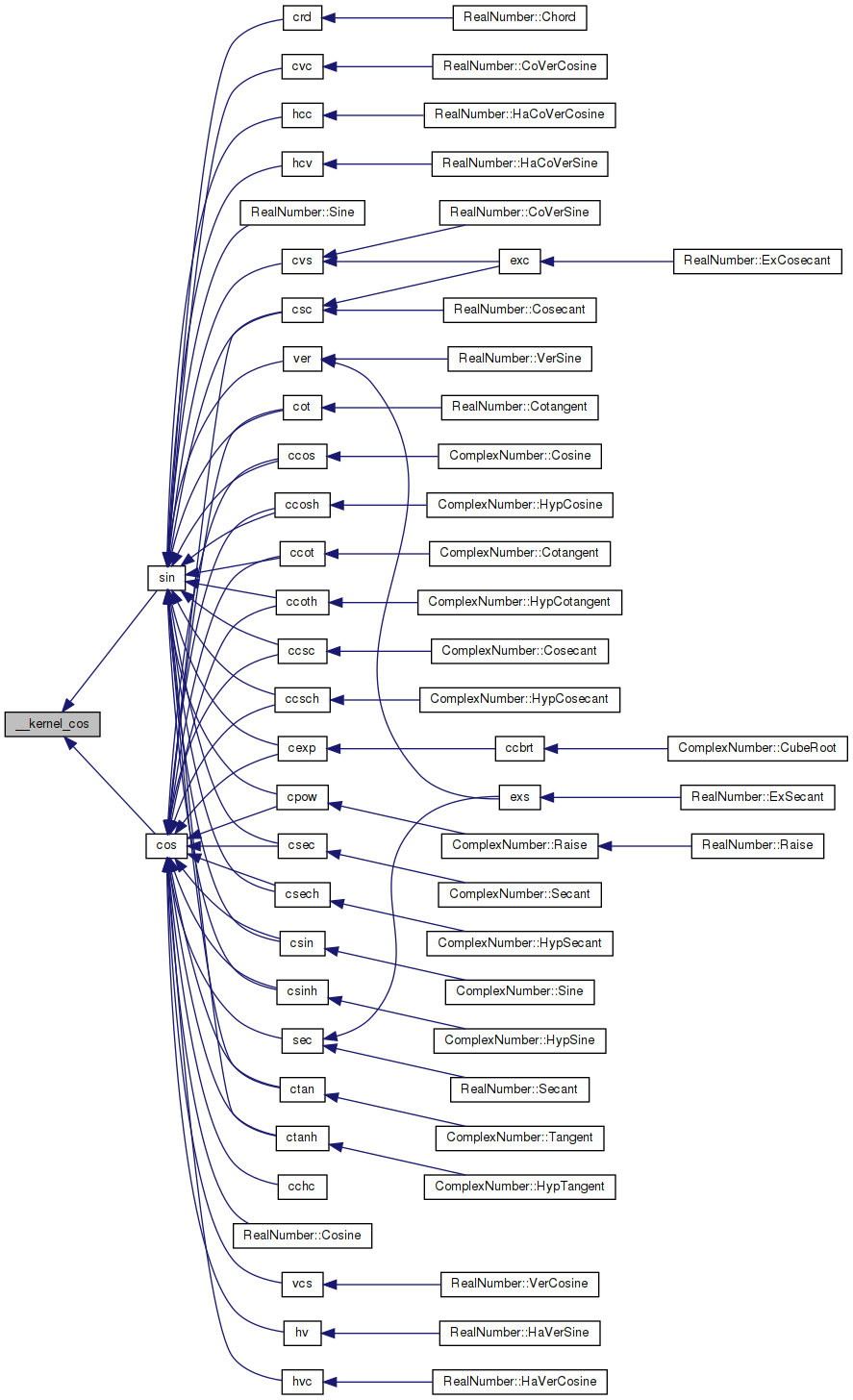
Referenced by cos(), and sin().
#define GET_HIGH_WORD(i, d)
Get the more significant 32 bit int from a double.
Definition: prim.h:167
Here is the caller graph for this function:
◆ __kernel_rem_pio2()
| int __kernel_rem_pio2 | ( | double * | x, |
| double * | y, | ||
| int | e0, | ||
| int | nx, | ||
| int | prec, | ||
| const int * | ipio2 | ||
| ) |
Kernel reduction function.
__kernel_rem_pio2(x,y,e0,nx,prec,ipio2) double x[],y[]; int e0,nx,prec; int ipio2[];
__kernel_rem_pio2 return the last three digits of N with
y = x - N*pi/2
so that |y| < pi/2.The method is to compute the integer (mod 8) and fraction parts of (2/pi)*x without doing the full multiplication. In general we skip the part of the product that are known to be a huge integer ( more accurately, = 0 mod 8 ). Thus the number of operations are independent of the exponent of the input.
(2/pi) is represented by an array of 24-bit integers in ipio2[].
Input parameters:
x[] The input value (must be positive) is broken into nx
pieces of 24-bit integers in double precision format.
x[i] will be the i-th 24 bit of x. The scaled exponent
of x[0] is given in input parameter e0 (i.e., x[0]*2^e0
match x's up to 24 bits. Example of breaking a double positive z into x[0]+x[1]+x[2]:
e0 = ilogb(z)-23
z = scalbn(z,-e0)
for i = 0,1,2
x[i] = floor(z)
z = (z-x[i])*2**24 y[] ouput result in an array of double precision numbers.
The dimension of y[] is:
24-bit precision 1
53-bit precision 2
64-bit precision 2
113-bit precision 3
The actual value is the sum of them. Thus for 113-bit
precison, one may have to do something like: long double t,w,r_head, r_tail;
t = (long double)y[2] + (long double)y[1];
w = (long double)y[0];
r_head = t+w;
r_tail = w - (r_head - t);e0 The exponent of x[0]
nx dimension of x[]
prec an integer indicating the precision:
0 24 bits (single)
1 53 bits (double)
2 64 bits (extended)
3 113 bits (quad) ipio2[]
integer array, contains the (24*i)-th to (24*i+23)-th
bit of 2/pi after binary point. The corresponding
floating value is
ipio2[i] * 2^(-24(i+1)).
External function: double scalbn(), floor();
Here is the description of some local variables:jk jk+1 is the initial number of terms of ipio2[] needed in the computation. The recommended value is 2,3,4, 6 for single, double, extended,and quad. jz local integer variable indicating the number of terms of ipio2[] used.
jx nx - 1
jv index for pointing to the suitable ipio2[] for the
computation. In general, we want
( 2^e0*x[0] * ipio2[jv-1]*2^(-24jv) )/8
is an integer. Thus
e0-3-24*jv >= 0 or (e0-3)/24 >= jv
Hence jv = max(0,(e0-3)/24).jp jp+1 is the number of terms in PIo2[] needed, jp = jk.
q[] double array with integral value, representing the
24-bits chunk of the product of x and 2/pi. q0 the corresponding exponent of q[0]. Note that the
exponent for q[i] would be q0-24*i. PIo2[] double precision array, obtained by cutting pi/2
into 24 bits chunks.f[] ipio2[] in floating point
iq[] integer array by breaking up q[] in 24-bits chunk.
fq[] final product of x*(2/pi) in fq[0],..,fq[jk]
ih integer. If >0 it indicates q[] is >= 0.5, hence
it also indicates the sign of the result.
Definition at line 184 of file kremp2.c.
References floor(), init_jk, one, PIo2, scalbn(), two24, twon24, and zero.
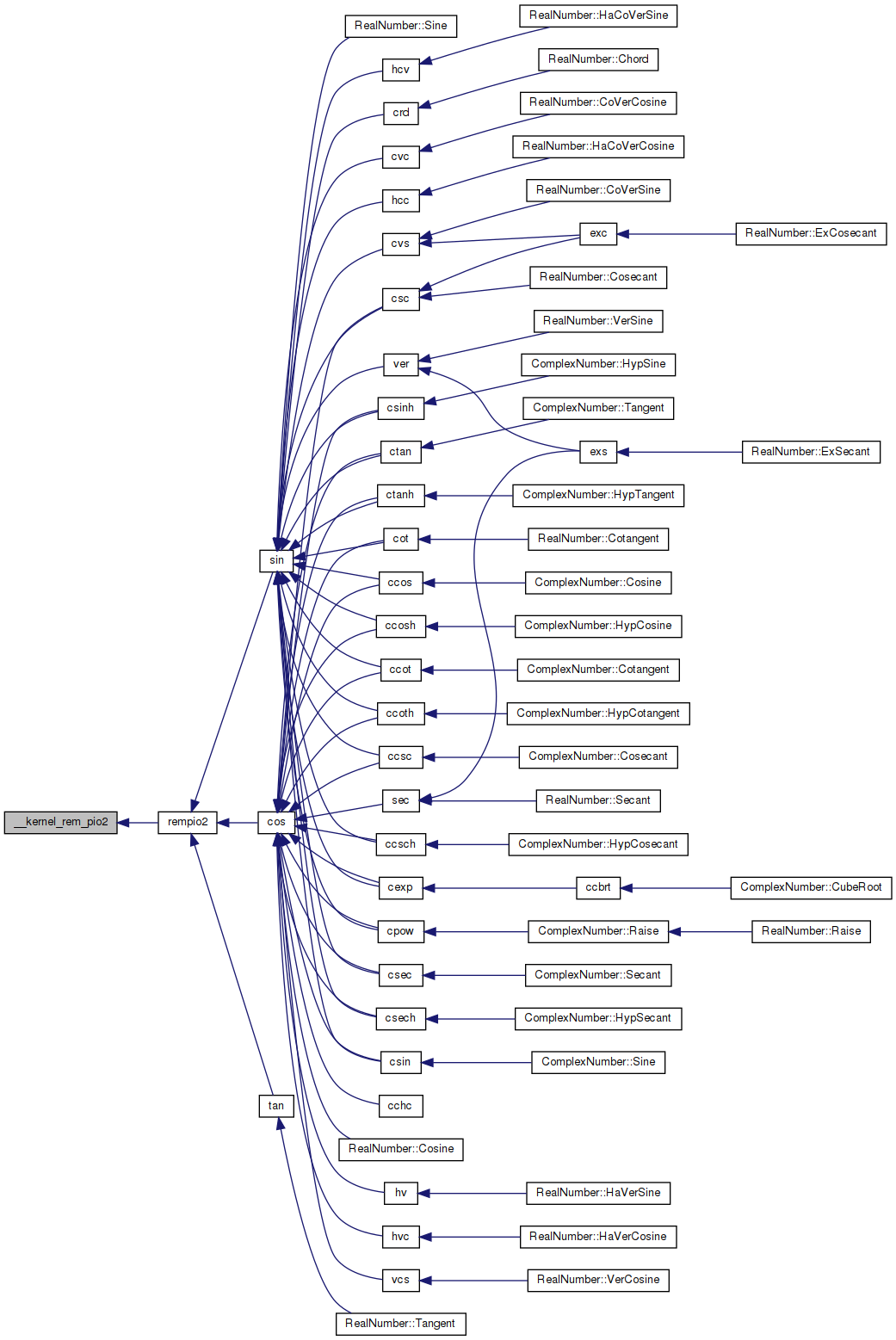
Referenced by rempio2().
double scalbn(double x, int n)
Here is the call graph for this function:
Here is the caller graph for this function:
◆ __kernel_sin()
| double __kernel_sin | ( | double | x, |
| double | y, | ||
| int | iy | ||
| ) |
Kernel sin function.
Kernel sin function on [-pi/4, pi/4], pi/4 ~ 0.7854 Input x is assumed to be bounded by ~pi/4 in magnitude. Input y is the tail of x. Input iy indicates whether y is 0. (if iy=0, y assume to be 0).
Algorithm
1. Since sin(-x) = -sin(x), we need only to consider positive x.
2. if x < 2^-27 (hx<0X3E400000 0), return x with inexact if x!=0.
3. sin(x) is approximated by a polynomial of degree 13 on [0,pi/4]
3 13
sin(x) ~ x + S1*x + ... + S6*xwhere
|sin(x) 2 4 6 8 10 12 | -58
|----- - (1+S1*x +S2*x +S3*x +S4*x +S5*x +S6*x )| <= 2
| x | 4. sin(x+y) = sin(x) + sin'(x')*y
~ sin(x) + (1-x*x/2)*y For better accuracy, let
3 2 2 2 2
r = x *(S2+x *(S3+x *(S4+x *(S5+x *S6))))
then 3 2
sin(x) = x + (S1*x + (x *(r-y/2)+y))
Definition at line 89 of file ksin.c.
References half, S1, S2, S3, S4, S5, and S6.
Referenced by cos(), and sin().
#define GET_HIGH_WORD(i, d)
Get the more significant 32 bit int from a double.
Definition: prim.h:167
Here is the caller graph for this function:
◆ __kernel_tan()
| double __kernel_tan | ( | double | x, |
| double | y, | ||
| int | iy | ||
| ) |
Kernel tan function.
Kernel tan function on [-pi/4, pi/4], pi/4 ~ 0.7854 Input x is assumed to be bounded by ~pi/4 in magnitude. Input y is the tail of x. Input k indicates whether tan (if k = 1) or -1/tan (if k = -1) is returned.
Algorithm
1. Since tan(-x) = -tan(x), we need only to consider positive x.
2. if x < 2^-28 (hx<0x3e300000 0), return x with inexact if x!=0.
3. tan(x) is approximated by a odd polynomial of degree 27 on
[0,0.67434]
3 27
tan(x) ~ x + T1*x + ... + T13*x
where
|tan(x) 2 4 26 | -59.2
|----- - (1+T1*x +T2*x +.... +T13*x )| <= 2
| x |
Note: tan(x+y) = tan(x) + tan'(x)*y
~ tan(x) + (1+x*x)*y
Therefore, for better accuracy in computing tan(x+y), let
3 2 2 2 2
r = x *(T2+x *(T3+x *(...+x *(T12+x *T13))))
then
3 2
tan(x+y) = x + (T1*x + (x *(r+y)+y)) 4. For x in [0.67434,pi/4], let y = pi/4 - x, then
tan(x) = tan(pi/4-y) = (1-tan(y))/(1+tan(y))
= 1 - 2*(tan(y) - (tan(y)^2)/(1+tan(y)))
Definition at line 108 of file ktan.c.
References fabs().
Referenced by tan().
#define GET_HIGH_WORD(i, d)
Get the more significant 32 bit int from a double.
Definition: prim.h:167
#define SET_LOW_WORD(d, v)
Set the less significant 32 bits of a double from an int.
Definition: prim.h:209
Here is the call graph for this function:
Here is the caller graph for this function:
