Kernel reduction function. More...

#include "prim.h"

Include dependency graph for kremp2.c:

Functions
int	__kernel_rem_pio2 (double x, double y, int e0, int nx, int prec, const int *ipio2)
	Kernel reduction function. More...

Variables
static const int	init_jk [] = {2,3,4,6}

static const double	PIo2 []

static const double	zero = 0.0

static const double	one = 1.0

static const double	two24 = 1.67772160000000000000e+07

static const double	twon24 = 5.96046447753906250000e-08

Detailed Description

Kernel reduction function.

Definition in file kremp2.c.

Function Documentation

◆ __kernel_rem_pio2()

int __kernel_rem_pio2	(	double *	x,
		double *	y,
		int	e0,
		int	nx,
		int	prec,
		const int *	ipio2
	)

Kernel reduction function.

__kernel_rem_pio2(x,y,e0,nx,prec,ipio2)
double x[],y[]; int e0,nx,prec; int ipio2[];

__kernel_rem_pio2 return the last three digits of N with
    y = x - N*pi/2
so that |y| < pi/2.

The method is to compute the integer (mod 8) and fraction parts of
(2/pi)*x without doing the full multiplication. In general we
skip the part of the product that are known to be a huge integer (
more accurately, = 0 mod 8 ). Thus the number of operations are
independent of the exponent of the input.

(2/pi) is represented by an array of 24-bit integers in ipio2[].

Input parameters:
    x[] The input value (must be positive) is broken into nx
    pieces of 24-bit integers in double precision format.
    x[i] will be the i-th 24 bit of x. The scaled exponent
    of x[0] is given in input parameter e0 (i.e., x[0]*2^e0
    match x's up to 24 bits.

    Example of breaking a double positive z into x[0]+x[1]+x[2]:
        e0 = ilogb(z)-23
        z  = scalbn(z,-e0)
    for i = 0,1,2
        x[i] = floor(z)
        z    = (z-x[i])*2**24

 y[]    ouput result in an array of double precision numbers.
    The dimension of y[] is:
        24-bit  precision   1
        53-bit  precision   2
        64-bit  precision   2
        113-bit precision   3
    The actual value is the sum of them. Thus for 113-bit
    precison, one may have to do something like:

    long double t,w,r_head, r_tail;
    t = (long double)y[2] + (long double)y[1];
    w = (long double)y[0];
    r_head = t+w;
    r_tail = w - (r_head - t);

 e0 The exponent of x[0]

 nx dimension of x[]

    prec    an integer indicating the precision:
        0   24  bits (single)
        1   53  bits (double)
        2   64  bits (extended)
        3   113 bits (quad)

 ipio2[]
    integer array, contains the (24*i)-th to (24*i+23)-th
    bit of 2/pi after binary point. The corresponding
    floating value is
ipio2[i] * 2^(-24(i+1)).

External function:
 double scalbn(), floor();

Here is the description of some local variables:
jk  jk+1 is the initial number of terms of ipio2[] needed
in the computation. The recommended value is 2,3,4,
6 for single, double, extended,and quad.

jz  local integer variable indicating the number of
terms of ipio2[] used.

 jx nx - 1

 jv index for pointing to the suitable ipio2[] for the
    computation. In general, we want
        ( 2^e0*x[0] * ipio2[jv-1]*2^(-24jv) )/8
    is an integer. Thus
        e0-3-24*jv >= 0 or (e0-3)/24 >= jv
    Hence jv = max(0,(e0-3)/24).

 jp jp+1 is the number of terms in PIo2[] needed, jp = jk.

    q[] double array with integral value, representing the
    24-bits chunk of the product of x and 2/pi.

 q0 the corresponding exponent of q[0]. Note that the
    exponent for q[i] would be q0-24*i.

 PIo2[] double precision array, obtained by cutting pi/2
    into 24 bits chunks.

 f[]    ipio2[] in floating point

 iq[]   integer array by breaking up q[] in 24-bits chunk.

 fq[]   final product of x*(2/pi) in fq[0],..,fq[jk]

 ih integer. If >0 it indicates q[] is >= 0.5, hence
    it also indicates the sign of the result.

Definition at line 184 of file kremp2.c.

References floor(), init_jk, one, PIo2, scalbn(), two24, twon24, and zero.

Referenced by rempio2().

 {
     int jz,jx,jv,jp,jk,carry,n,iq[20],i,j,k,m,q0,ih;
     double z,fw,f[20],fq[20],q[20];
 
     /* initialize jk*/
     jk = init_jk[prec];
     jp = jk;
 
     /* determine jx,jv,q0, note that 3>q0 */
     jx =  nx-1;
     jv = (e0-3)/24;
     if(jv<0) jv=0;
     q0 =  e0-24*(jv+1);
 
     /* set up f[0] to f[jx+jk] where f[jx+jk] = ipio2[jv+jk] */
     j = jv-jx;
     m = jx+jk;
     for(i=0; i<=m; i++,j++) f[i] = (j<0)? zero : (double) ipio2[j];
 
     /* compute q[0],q[1],...q[jk] */
     for (i=0; i<=jk; i++) {
         for(j=0,fw=0.0; j<=jx; j++) fw += x[j]*f[jx+i-j];
         q[i] = fw;
     }
 
     jz = jk;
 recompute:
     /* distill q[] into iq[] reversingly */
     for(i=0,j=jz,z=q[jz]; j>0; i++,j--) {
         fw    =  (double)((int)(twon24* z));
         iq[i] =  (int)(z-two24*fw);
         z     =  q[j-1]+fw;
     }
 
     /* compute n */
     z  = scalbn(z,q0);      /* actual value of z */
     z -= 8.0*floor(z*0.125);        /* trim off integer >= 8 */
     n  = (int) z;
     z -= (double)n;
     ih = 0;
     if(q0>0) {  /* need iq[jz-1] to determine n */
         i  = (iq[jz-1]>>(24-q0));
         n += i;
         iq[jz-1] -= i<<(24-q0);
         ih = iq[jz-1]>>(23-q0);
     }
     else if(q0==0) ih = iq[jz-1]>>23;
     else if(z>=0.5) ih=2;
 
     if(ih>0) {  /* q > 0.5 */
         n += 1;
         carry = 0;
         for(i=0; i<jz ; i++) {  /* compute 1-q */
             j = iq[i];
             if(carry==0) {
                 if(j!=0) {
                     carry = 1;
                     iq[i] = 0x1000000- j;
                 }
             } else  iq[i] = 0xffffff - j;
         }
         if(q0>0) {      /* rare case: chance is 1 in 12 */
             switch(q0) {
             case 1:
                 iq[jz-1] &= 0x7fffff;
                 break;
             case 2:
                 iq[jz-1] &= 0x3fffff;
                 break;
             }
         }
         if(ih==2) {
             z = one - z;
             if(carry!=0) z -= scalbn(one,q0);
         }
     }
 
     /* check if recomputation is needed */
     if(z==zero) {
         j = 0;
         for (i=jz-1; i>=jk; i--) j |= iq[i];
         if(j==0) { /* need recomputation */
             for(k=1; iq[jk-k]==0; k++); /* k = no. of terms needed */
 
             for(i=jz+1; i<=jz+k; i++) { /* add q[jz+1] to q[jz+k] */
                 f[jx+i] = (double) ipio2[jv+i];
                 for(j=0,fw=0.0; j<=jx; j++) fw += x[j]*f[jx+i-j];
                 q[i] = fw;
             }
             jz += k;
             goto recompute;
         }
     }
 
     /* chop off zero terms */
     if(z==0.0) {
         jz -= 1;
         q0 -= 24;
         while(iq[jz]==0) {
             jz--;
             q0-=24;
         }
     } else { /* break z into 24-bit if necessary */
         z = scalbn(z,-q0);
         if(z>=two24) {
             fw = (double)((int)(twon24*z));
             iq[jz] = (int)(z-two24*fw);
             jz += 1;
             q0 += 24;
             iq[jz] = (int) fw;
         } else iq[jz] = (int) z ;
     }
 
     /* convert integer "bit" chunk to floating-point value */
     fw = scalbn(one,q0);
     for(i=jz; i>=0; i--) {
         q[i] = fw*(double)iq[i];
         fw*=twon24;
     }
 
     /* compute PIo2[0,...,jp]*q[jz,...,0] */
     for(i=jz; i>=0; i--) {
         for(fw=0.0,k=0; k<=jp&&k<=jz-i; k++) fw += PIo2[k]*q[i+k];
         fq[jz-i] = fw;
     }
 
     /* compress fq[] into y[] */
     switch(prec) {
     case 0:
         fw = 0.0;
         for (i=jz; i>=0; i--) fw += fq[i];
         y[0] = (ih==0)? fw: -fw;
         break;
     case 1:
     case 2:
         fw = 0.0;
         for (i=jz; i>=0; i--) fw += fq[i];
         y[0] = (ih==0)? fw: -fw;
         fw = fq[0]-fw;
         for (i=1; i<=jz; i++) fw += fq[i];
         y[1] = (ih==0)? fw: -fw;
         break;
     case 3: /* painful */
         for (i=jz; i>0; i--) {
             fw      = fq[i-1]+fq[i];
             fq[i]  += fq[i-1]-fw;
             fq[i-1] = fw;
         }
         for (i=jz; i>1; i--) {
             fw      = fq[i-1]+fq[i];
             fq[i]  += fq[i-1]-fw;
             fq[i-1] = fw;
         }
         for (fw=0.0,i=jz; i>=2; i--) fw += fq[i];
         if(ih==0) {
             y[0] =  fq[0];
             y[1] =  fq[1];
             y[2] =  fw;
         } else {
             y[0] = -fq[0];
             y[1] = -fq[1];
             y[2] = -fw;
         }
     }
     return n&7;
 }

Here is the call graph for this function:

Here is the caller graph for this function:

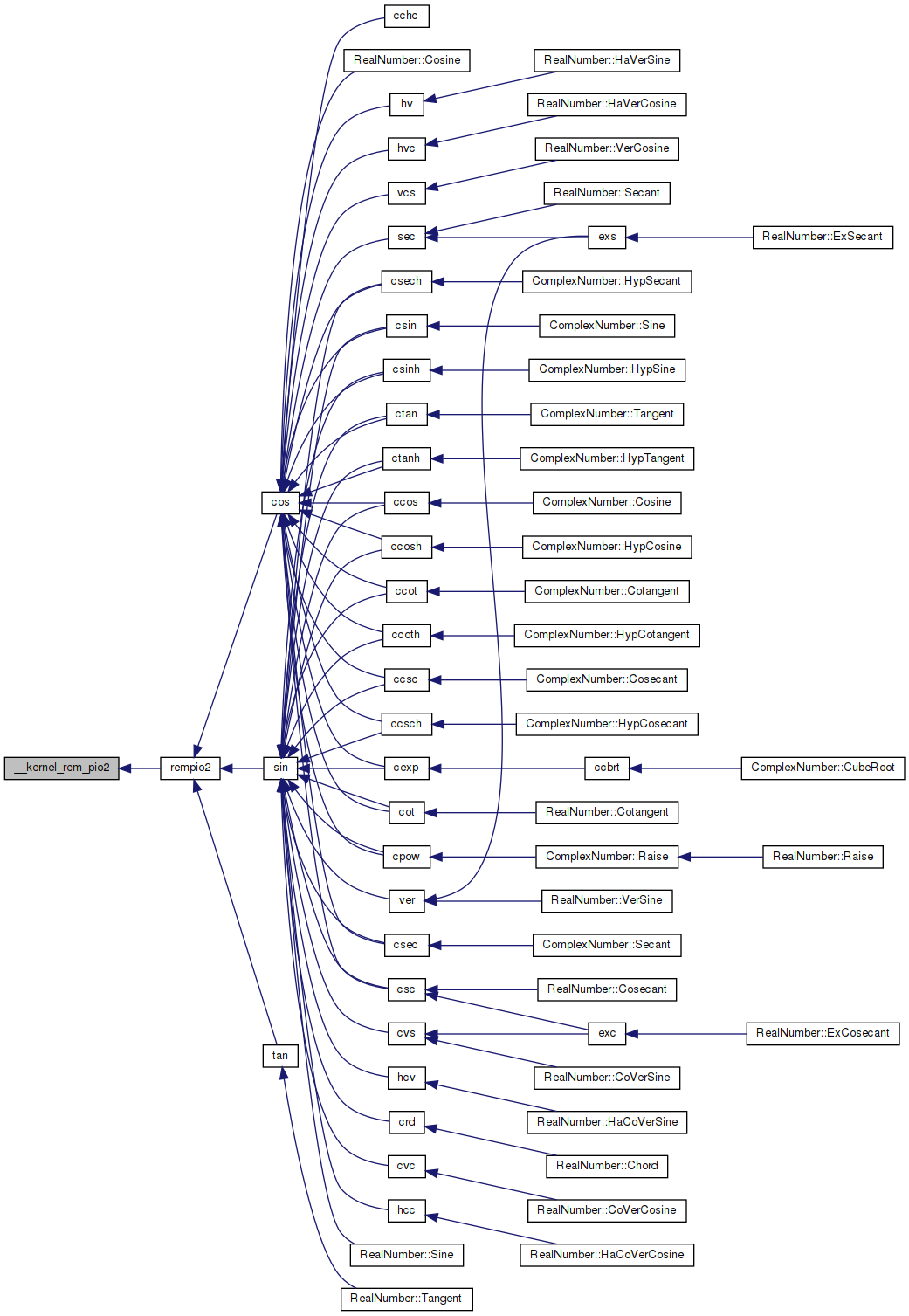
Variable Documentation

◆ init_jk

const int init_jk[] = {2,3,4,6}

static

Definition at line 56 of file kremp2.c.

Referenced by __kernel_rem_pio2().

◆ one

const double one = 1.0

static

Definition at line 71 of file kremp2.c.

Referenced by __kernel_rem_pio2().

◆ PIo2

const double PIo2[]

static

Initial value:

= {
57079625129699707031e+00, 
54978941586159635335e-08, 
39030252995776476554e-15, 
28200341580791294123e-22, 
27065575308067607349e-29, 
22933308981111328932e-36, 
73370053816464559624e-44, 
16741683877804819444e-51, 
}

Definition at line 58 of file kremp2.c.

Referenced by __kernel_rem_pio2().

◆ two24

const double two24 = 1.67772160000000000000e+07

static

Definition at line 72 of file kremp2.c.

Referenced by __kernel_rem_pio2().

◆ twon24

const double twon24 = 5.96046447753906250000e-08

static

Definition at line 73 of file kremp2.c.

Referenced by __kernel_rem_pio2().

◆ zero

const double zero = 0.0

static

Definition at line 70 of file kremp2.c.

Referenced by __kernel_rem_pio2().

Functions

Variables

Detailed Description

Function Documentation

◆ __kernel_rem_pio2()

Variable Documentation

◆ init_jk

◆ one

◆ PIo2

◆ two24

◆ twon24

◆ zero