ksin.c File Reference

Kernel sin function. More...

#include "prim.h"

Include dependency graph for ksin.c:

Go to the source code of this file.

Functions
double	__kernel_sin (double x, double y, int iy)
	Kernel sin function. More...

Variables
static const double	half = 5.00000000000000000000e-01
static const double	S1 = -1.66666666666666324348e-01
static const double	S2 = 8.33333333332248946124e-03
static const double	S3 = -1.98412698298579493134e-04
static const double	S4 = 2.75573137070700676789e-06
static const double	S5 = -2.50507602534068634195e-08
static const double	S6 = 1.58969099521155010221e-10

Detailed Description

Kernel sin function.

Definition in file ksin.c.

Function Documentation

__kernel_sin()

double __kernel_sin	(	double	x,
		double	y,
		int	iy
	)

Kernel sin function.

Kernel sin function on [-pi/4, pi/4], pi/4 ~ 0.7854
Input x is assumed to be bounded by ~pi/4 in magnitude.
Input y is the tail of x.
Input iy indicates whether y is 0. (if iy=0, y assume to be 0).

Algorithm
  1. Since sin(-x) = -sin(x), we need only to consider positive x.
  2. if x < 2^-27 (hx<0X3E400000 0), return x with inexact if x!=0.
  3. sin(x) is approximated by a polynomial of degree 13 on [0,pi/4]
                       3            13
      sin(x) ~ x + S1*x + ... + S6*x

    where

    |sin(x)         2     4     6     8     10     12  |     -58
    |----- - (1+S1*x +S2*x +S3*x +S4*x +S5*x  +S6*x   )| <= 2
    |  x                                               |

  4. sin(x+y) = sin(x) + sin'(x')*y
              ~ sin(x) + (1-x*x/2)*y

       For better accuracy, let
          3      2      2      2      2
      r = x *(S2+x *(S3+x *(S4+x *(S5+x *S6))))
    then                3    2
      sin(x) = x + (S1*x + (x *(r-y/2)+y))

Definition at line 89 of file ksin.c.

References half, S1, S2, S3, S4, S5, and S6.

Referenced by cos(), and sin().

{
    double z, r, v;
    int32_t ix;

    GET_HIGH_WORD(ix, x);
    ix &= 0x7FFFFFFF;

    // |x| < 2**-27
    if (ix < 0x3E400000)
    {
        // generate inexact
        if ((int)x == 0)
        {
            return x;
        }
    }

    z = x * x;
    v = z * x;
    r = S2 + z * (S3 + z * (S4 + z * (S5 + z * S6)));

    if (iy == 0)
    {
        return x + v * (S1 + z * r);
    }

    return x - ((z * (half * y - v * r) - y) - v * S1);
}

Here is the caller graph for this function:

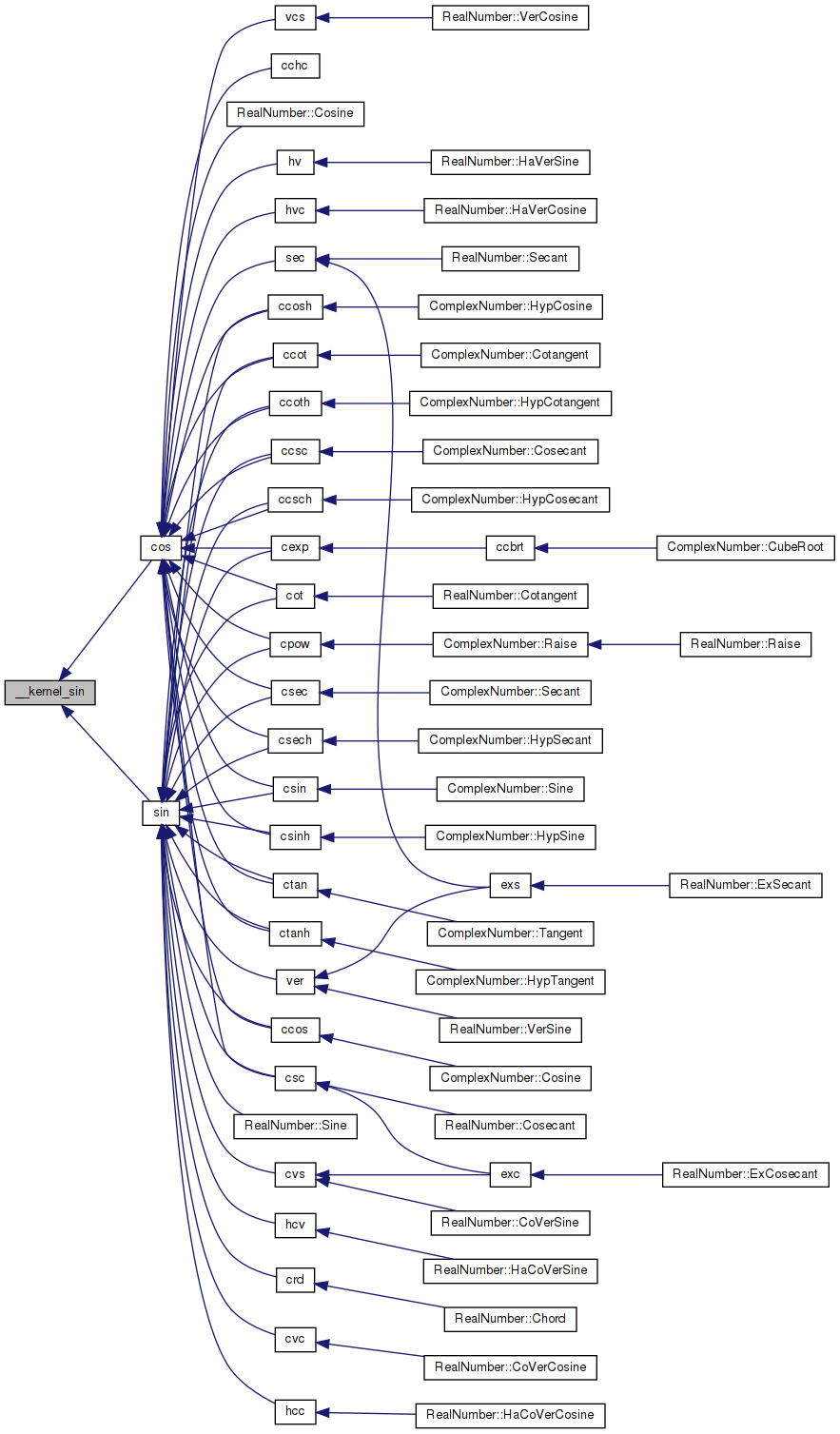
Variable Documentation

half

const double half = 5.00000000000000000000e-01

static

Definition at line 49 of file ksin.c.

Referenced by __kernel_sin().

S1

const double S1 = -1.66666666666666324348e-01

static

Definition at line 50 of file ksin.c.

Referenced by __kernel_sin().

S2

const double S2 = 8.33333333332248946124e-03

static

Definition at line 51 of file ksin.c.

Referenced by __kernel_sin().

S3

const double S3 = -1.98412698298579493134e-04

static

Definition at line 52 of file ksin.c.

Referenced by __kernel_sin().

S4

const double S4 = 2.75573137070700676789e-06

static

Definition at line 53 of file ksin.c.

Referenced by __kernel_sin().

S5

const double S5 = -2.50507602534068634195e-08

static

Definition at line 54 of file ksin.c.

Referenced by __kernel_sin().

S6

const double S6 = 1.58969099521155010221e-10

static

Definition at line 55 of file ksin.c.

Referenced by __kernel_sin().