kcos.c File Reference

Kernel cosine function. More...

#include "prim.h"

Include dependency graph for kcos.c:

Go to the source code of this file.

Functions
double	__kernel_cos (double x, double y)
	Kernel cosine function. More...

Variables
static const double	one = 1.00000000000000000000e+00
static const double	C1 = 4.16666666666666019037e-02
static const double	C2 = -1.38888888888741095749e-03
static const double	C3 = 2.48015872894767294178e-05
static const double	C4 = -2.75573143513906633035e-07
static const double	C5 = 2.08757232129817482790e-09
static const double	C6 = -1.13596475577881948265e-11

Detailed Description

Kernel cosine function.

Definition in file kcos.c.

Function Documentation

__kernel_cos()

double __kernel_cos	(	double	x,
		double	y
	)

Kernel cosine function.

Kernel cos function on [-pi/4, pi/4], pi/4 ~ 0.785398164
Input x is assumed to be bounded by ~pi/4 in magnitude.
Input y is the tail of x.

Algorithm
 1. Since cos(-x) = cos(x), we need only to consider positive x.
 2. if x < 2^-27 (hx<0x3e400000 0), return 1 with inexact if x!=0.
 3. cos(x) is approximated by a polynomial of degree 14 on
    [0,pi/4]
                         4            14
        cos(x) ~ 1 - x*x/2 + C1*x + ... + C6*x
    where the Remes error is

    |              2     4     6     8     10    12     14 |     -58
    |cos(x)-(1-.5*x +C1*x +C2*x +C3*x +C4*x +C5*x  +C6*x  )| <= 2
    |                                      |
           4     6     8     10    12     14

 4. let r = C1*x +C2*x +C3*x +C4*x +C5*x  +C6*x  , then
        cos(x) = 1 - x*x/2 + r
    since cos(x+y) ~ cos(x) - sin(x)*y
          ~ cos(x) - x*y,
    a correction term is necessary in cos(x) and hence
    cos(x+y) = 1 - (x*x/2 - (r - x*y))
    For better accuracy when x > 0.3, let qx = |x|/4 with
    the last 32 bits mask off, and if x > 0.78125, let qx = 0.28125.
    Then
    cos(x+y) = (1-qx) - ((x*x/2-qx) - (r-x*y)).
    Note that 1-qx and (x*x/2-qx) is EXACT here, and the
    magnitude of the latter is at least a quarter of x*x/2,
    thus, reducing the rounding error in the subtraction.

Definition at line 94 of file kcos.c.

References C1, C2, C3, C4, C5, C6, and one.

Referenced by cos(), and sin().

{
    double a, hz, z, r, qx;
    int32_t ix;

    GET_HIGH_WORD(ix, x);
    ix &= 0x7FFFFFFF;

    // if x < 2**27
    if (ix < 0x3E400000)
    {
        // generate inexact
        if ((int)x == 0)
        {
            return one;
        }
    }

    z = x * x;
    r = z * (C1 + z * (C2 + z * (C3 + z * (C4 + z * (C5 + z * C6)))));

    // |x| < 0.3
    if (ix < 0x3FD33333)
    {
        return one - (0.5 * z - (z * r - x * y));
    }

    // x > 0.78125
    if (ix > 0x3FE90000)
    {
        qx = 0.28125;
    }
    else
    {
        INSERT_WORDS(qx, ix - 0x00200000, 0);
    }

    hz = 0.5 * z - qx;
    a = one - qx;
    return a - (hz - (z * r - x * y));
}

Here is the caller graph for this function:

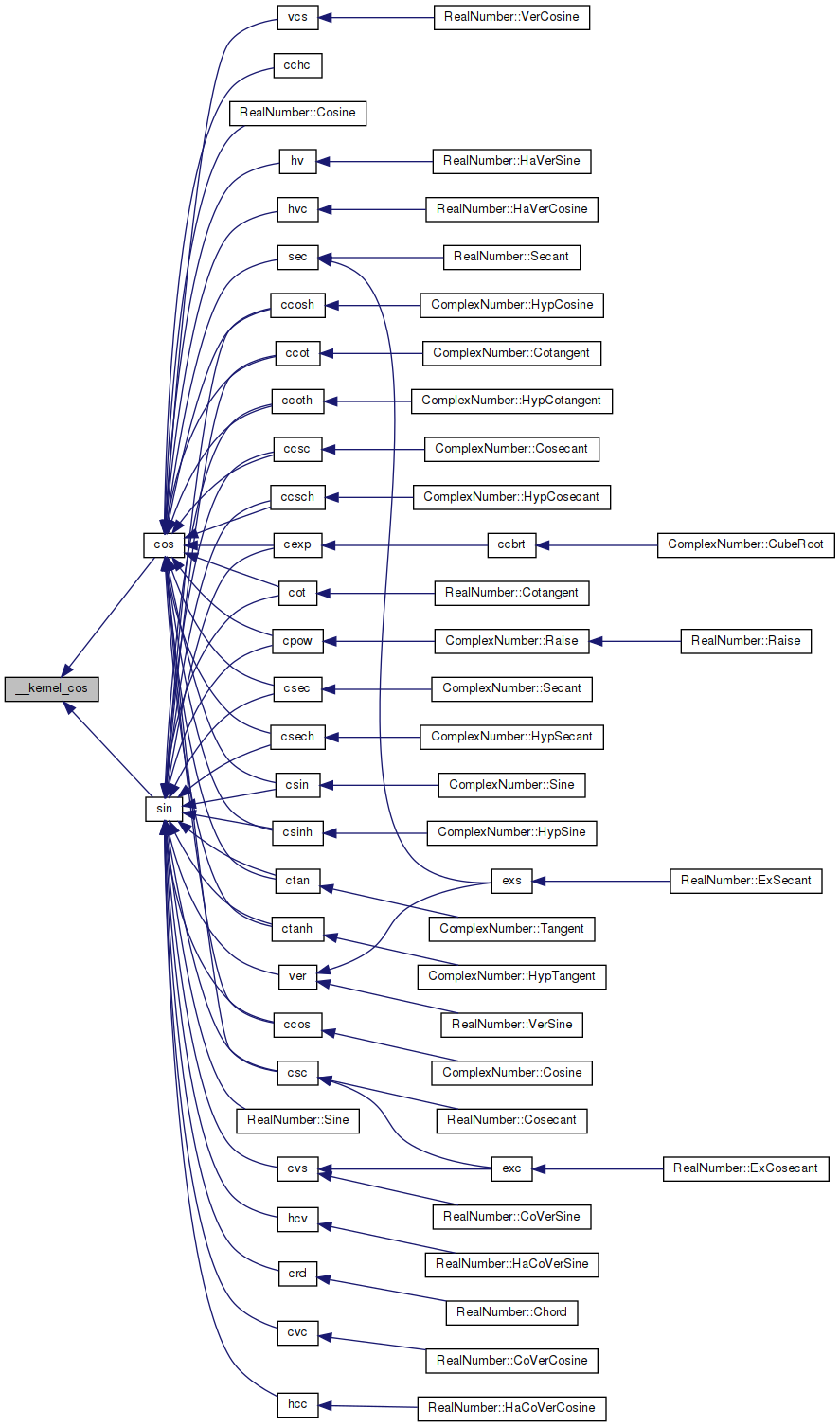
Variable Documentation

C1

const double C1 = 4.16666666666666019037e-02

static

Definition at line 50 of file kcos.c.

Referenced by __kernel_cos().

C2

const double C2 = -1.38888888888741095749e-03

static

Definition at line 51 of file kcos.c.

Referenced by __kernel_cos().

C3

const double C3 = 2.48015872894767294178e-05

static

Definition at line 52 of file kcos.c.

Referenced by __kernel_cos().

C4

const double C4 = -2.75573143513906633035e-07

static

Definition at line 53 of file kcos.c.

Referenced by __kernel_cos().

C5

const double C5 = 2.08757232129817482790e-09

static

Definition at line 54 of file kcos.c.

Referenced by __kernel_cos().

C6

const double C6 = -1.13596475577881948265e-11

static

Definition at line 55 of file kcos.c.

Referenced by __kernel_cos().

one

const double one = 1.00000000000000000000e+00

static

Definition at line 49 of file kcos.c.

Referenced by __kernel_cos().