Returns the exponential of x.
Method
1. Argument reduction:
Reduce x to an r so that |r| <= 0.5*ln2 ~ 0.34658.
Given x, find r and integer k such that
x = k*ln2 + r, |r| <= 0.5*ln2.
Here r will be represented as r = hi-lo for better
accuracy.
2. Approximation of exp(r) by a special rational function on
the interval [0,0.34658]:
Write
R(r**2) = r*(exp(r)+1)/(exp(r)-1) = 2 + r*r/6 - r**4/360 + ...
We use a special Remes algorithm on [0,0.34658] to generate
a polynomial of degree 5 to approximate R. The maximum error
of this polynomial approximation is bounded by 2**-59. In
other words,
R(z) ~ 2.0 + P1*z + P2*z**2 + P3*z**3 + P4*z**4 + P5*z**5
(where z=r*r, and the values of P1 to P5 are listed below)
and
| 5 | -59
| 2.0+P1*z+...+P5*z - R(z) | <= 2
| |
The computation of exp(r) thus becomes
2*r
exp(r) = 1 + -------
R - r
r*R1(r)
= 1 + r + ----------- (for better accuracy)
2 - R1(r)
where
2 4 10
R1(r) = r - (P1*r + P2*r + ... + P5*r ).
3. Scale back to obtain exp(x):
From step 1, we have
exp(x) = 2^k * exp(r)
Special cases:
exp(INF) is INF, exp(NaN) is NaN;
exp(-INF) is 0, and
for finite argument, only exp(0)=1 is exact.
Accuracy:
according to an error analysis, the error is always less than
1 ulp (unit in the last place).
Misc. info:
For IEEE double
if x > 7.09782712893383973096e+02 then exp(x) overflow
if x < -7.45133219101941108420e+02 then exp(x) underflow
Constants:
The hexadecimal values are the intended ones for the following
constants. The decimal values may be used, provided that the
compiler will convert from decimal to binary accurately enough
to produce the hexadecimal values shown.
Definition at line 138 of file exp.c.
References halF, huge, invln2, ln2HI, ln2LO, o_threshold, one, P1, P2, P3, P4, P5, twom1000, and u_threshold.
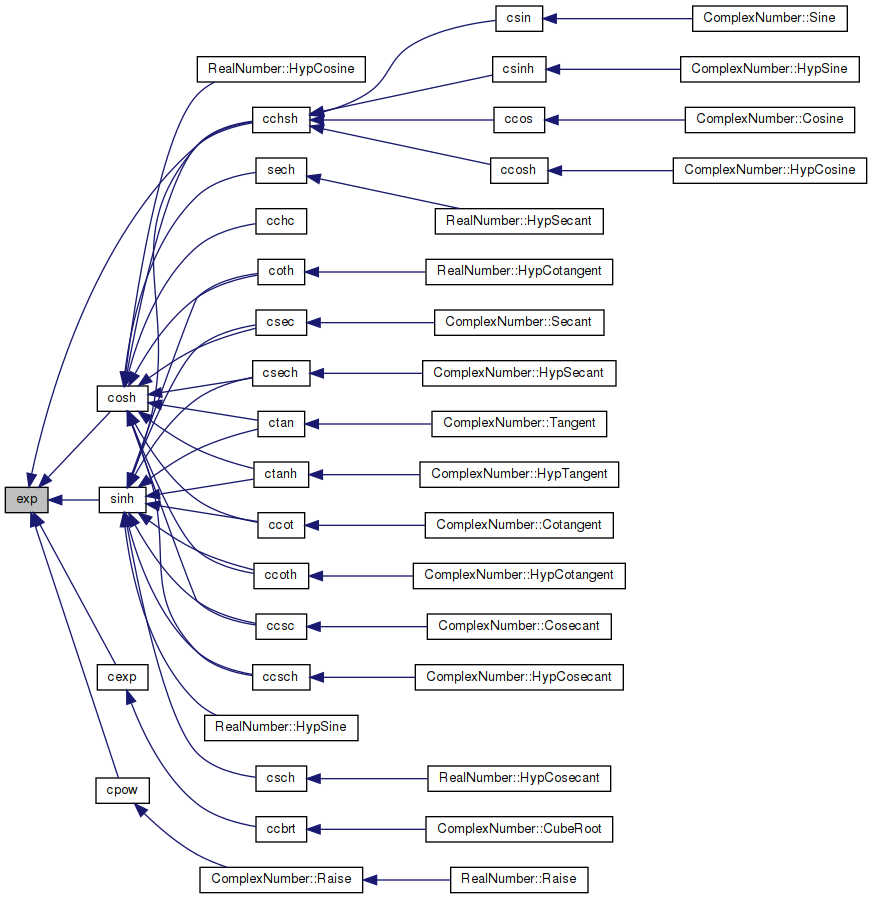
Referenced by cchsh(), cexp(), cosh(), cpow(), and sinh().
140 double y, hi, lo, c, t;
148 xsb = (hx >> 31) & 1;
153 if (hx >= 0x40862E42)
155 if (hx >= 0x7FF00000)
159 if (((hx & 0xFFFFF) | lx) != 0)
165 return (xsb == 0) ? x : 0.0;
196 hi = x - t *
ln2HI[0];
202 else if (hx < 0x3E300000)
220 c = x - t * (
P1 + t * (
P2 + t * (
P3 + t * (
P4 + t *
P5))));
223 return one - ((x * c) / (c - 2.0) - x);
226 y =
one - ((lo - (x * c) / (2.0 - c)) - hi);
static const double halF[2]
#define GET_HIGH_WORD(i, d)
Get the more significant 32 bit int from a double.
static const double u_threshold
#define GET_LOW_WORD(i, d)
Get the less significant 32 bit int from a double.
static const double ln2LO[2]
static const double ln2HI[2]
static const double twom1000
static const double o_threshold
static const double invln2
#define SET_HIGH_WORD(d, v)
Set the more significant 32 bits of a double from an int.