cacoth.c File Reference

#include "prim.h"

Include dependency graph for cacoth.c:

Go to the source code of this file.

Functions
complex	cacoth (complex z)
	Inverse hyperbolic cotangent of complex number. More...

Function Documentation

cacoth()

complex cacoth

(

complex

z

)

Inverse hyperbolic cotangent of complex number.

Inverse hyperbolic cotangent expressed using complex logarithms:

acoth(z) = 1/2 * ((log(z + 1) - log(z - 1))

More info is available at Wikipedia:
https://wikipedia.org/wiki/Inverse_hyperbolic_function#Logarithmic_representation

Definition at line 42 of file cacoth.c.

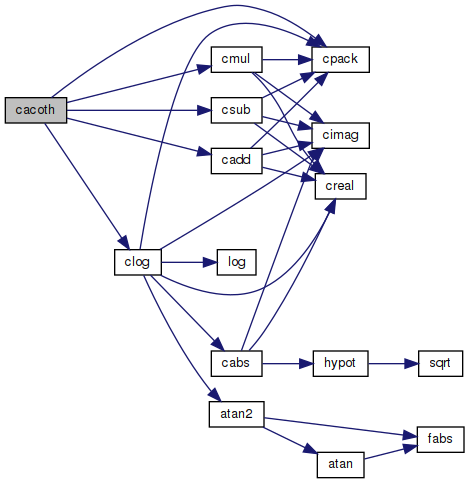
References cadd(), clog(), cmul(), cpack(), and csub().

Referenced by ComplexNumber::HypArcCotangent().

{
    complex half = cpack(0.5, 0.0);
    complex one = cpack(1.0, 0.0);
    complex a = clog(cadd(z, one));
    complex b = clog(csub(z, one));
    complex c = csub(a, b);
    complex w = cmul(half, c);
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function: