prim.c File Reference

#include "prim.h"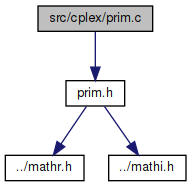

Include dependency graph for prim.c:

Go to the source code of this file.

Macros
#define	REAL_PART(z)   ((z).parts[0])
#define	IMAG_PART(z)   ((z).parts[1])

Functions
double	creal (complex z)
	Real part of complex number. More...
double	cimag (complex z)
	Imaginary part of complex number. More...
double	cabs (complex z)
	Absolute value of complex number. More...
complex	conj (complex z)
complex	cpack (double x, double y)
	Pack two real numbers into a complex number. More...
complex	ctrunc (complex z)
	Truncated value of complex number. More...
complex	cfloor (complex z)
	Floor value of complex number. More...
complex	cceil (complex z)
	Ceiling value of complex number. More...
complex	cround (complex z)
	Division of two complex numbers. More...
complex	cadd (complex y, complex z)
	Addition of two complex numbers. More...
complex	csub (complex y, complex z)
	Subtraction of two complex numbers. More...
complex	cmul (complex y, complex z)
	Multiplication of two complex numbers. More...
complex	cdiv (complex y, complex z)
	Division of two complex numbers. More...
complex	creci (complex z)
	Reciprocal value of complex number. More...
void	cchsh (double x, double *c, double *s)
	Calculate cosh and sinh. More...
void	cchc (double x, double *ch, double *c)
	Calculate cosh and cos. More...

Macro Definition Documentation

IMAG_PART

#define IMAG_PART

(

z

)

((z).parts[1])

Definition at line 33 of file prim.c.

REAL_PART

#define REAL_PART

(

z

)

((z).parts[0])

Definition at line 32 of file prim.c.

Function Documentation

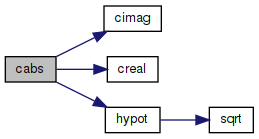
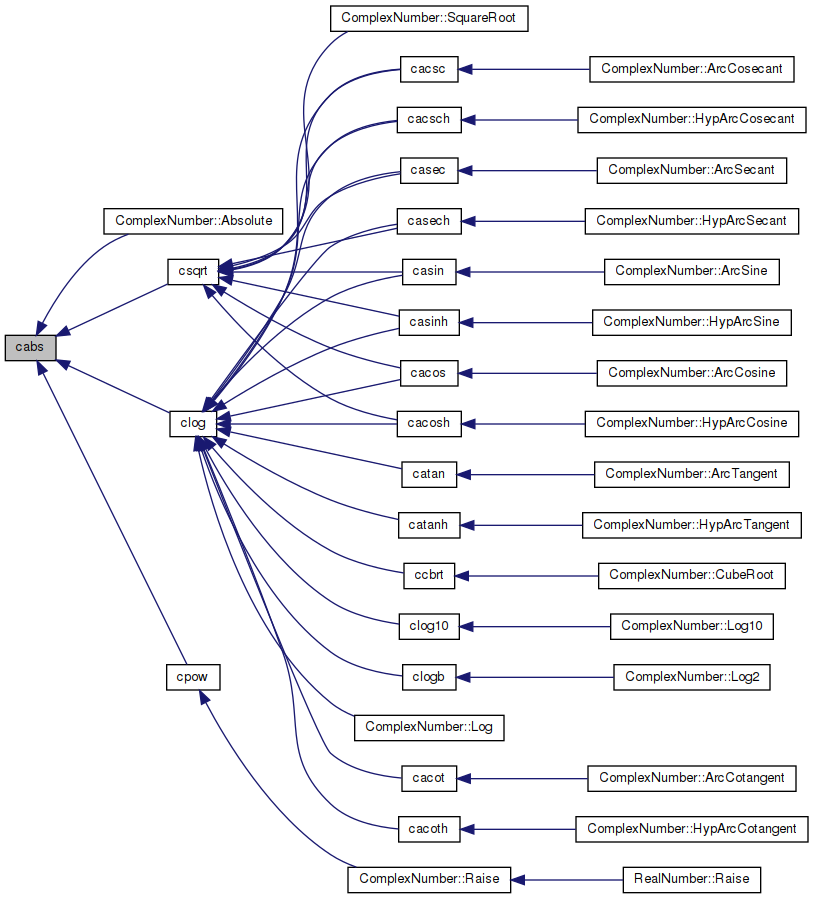
cabs()

double cabs

(

complex

z

)

Absolute value of complex number.

Definition at line 54 of file prim.c.

References cimag(), creal(), and hypot().

Referenced by ComplexNumber::Absolute(), clog(), cpow(), and csqrt().

{
    return hypot(creal(z), cimag(z));
}

Here is the call graph for this function:

Here is the caller graph for this function:

cadd()

complex cadd	(	complex	y,
		complex	z
	)

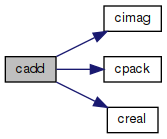
Addition of two complex numbers.

Definition at line 120 of file prim.c.

References cimag(), cpack(), and creal().

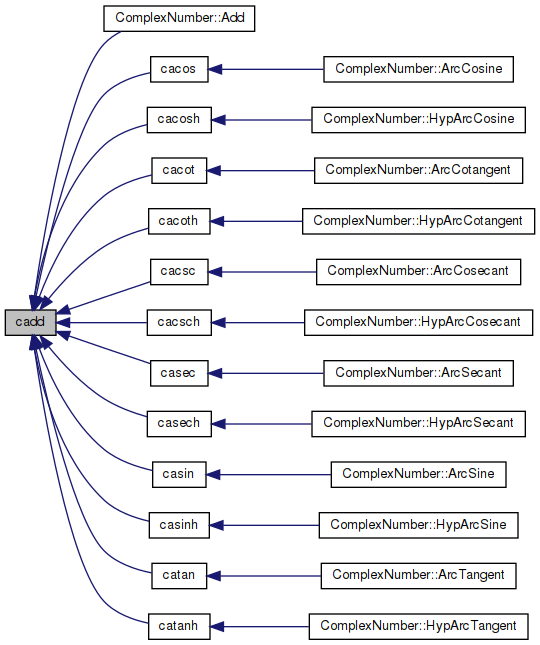
Referenced by ComplexNumber::Add(), cacos(), cacosh(), cacot(), cacoth(), cacsc(), cacsch(), casec(), casech(), casin(), casinh(), catan(), and catanh().

{
    complex w;
    w = cpack(creal(y) + creal(z), cimag(y) + cimag(z));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cceil()

complex cceil

(

complex

z

)

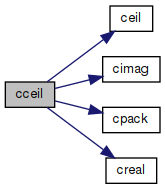
Ceiling value of complex number.

Definition at line 100 of file prim.c.

References ceil(), cimag(), cpack(), and creal().

Referenced by ComplexNumber::Ceiling().

{
    complex w;
    w = cpack(ceil(creal(z)), ceil(cimag(z)));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

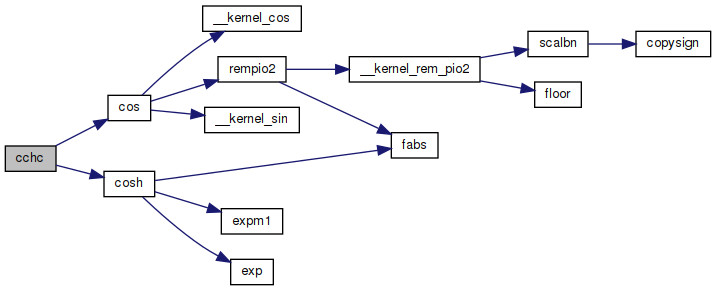
cchc()

void cchc	(	double	x,
		double *	ch,
		double *	c
	)

Calculate cosh and cos.

Definition at line 219 of file prim.c.

References cos(), and cosh().

{
    *ch = cosh(2.0 * x);
    *c = cos(2.0 * x);
}

Here is the call graph for this function:

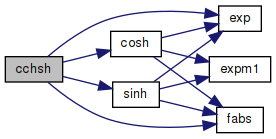
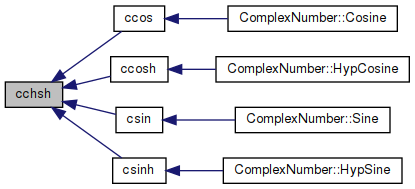
cchsh()

void cchsh	(	double	x,
		double *	c,
		double *	s
	)

Calculate cosh and sinh.

Definition at line 197 of file prim.c.

References cosh(), exp(), fabs(), and sinh().

Referenced by ccos(), ccosh(), csin(), and csinh().

{
    double e, ei;

    if (fabs(x) <= 0.5)
    {
        *c = cosh(x);
        *s = sinh(x);
    }
    else
    {
        e = exp(x);
        ei = 0.5 / e;
        e = 0.5 * e;
        *s = e - ei;
        *c = e + ei;
    }
}

Here is the call graph for this function:

Here is the caller graph for this function:

cdiv()

complex cdiv	(	complex	y,
		complex	z
	)

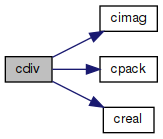
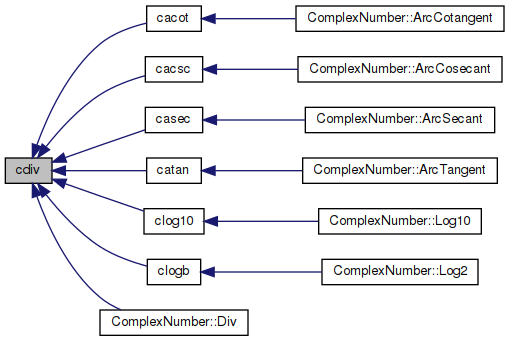
Division of two complex numbers.

Definition at line 159 of file prim.c.

References cimag(), cpack(), and creal().

Referenced by cacot(), cacsc(), casec(), catan(), clog10(), clogb(), and ComplexNumber::Div().

{
    complex w;
    double a, b, c, d;
    double q, v, x;

    a = creal(y);
    b = cimag(y);
    c = creal(z);
    d = cimag(z);

    q = c * c + d * d;
    v = a * c + b * d;
    x = b * c - a * d;

    w = cpack(v / q, x / q);
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cfloor()

complex cfloor

(

complex

z

)

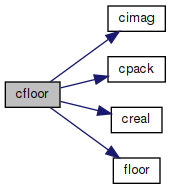
Floor value of complex number.

Definition at line 90 of file prim.c.

References cimag(), cpack(), creal(), and floor().

Referenced by ComplexNumber::Floor().

{
    complex w;
    w = cpack(floor(creal(z)), floor(cimag(z)));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cimag()

double cimag

(

complex

z

)

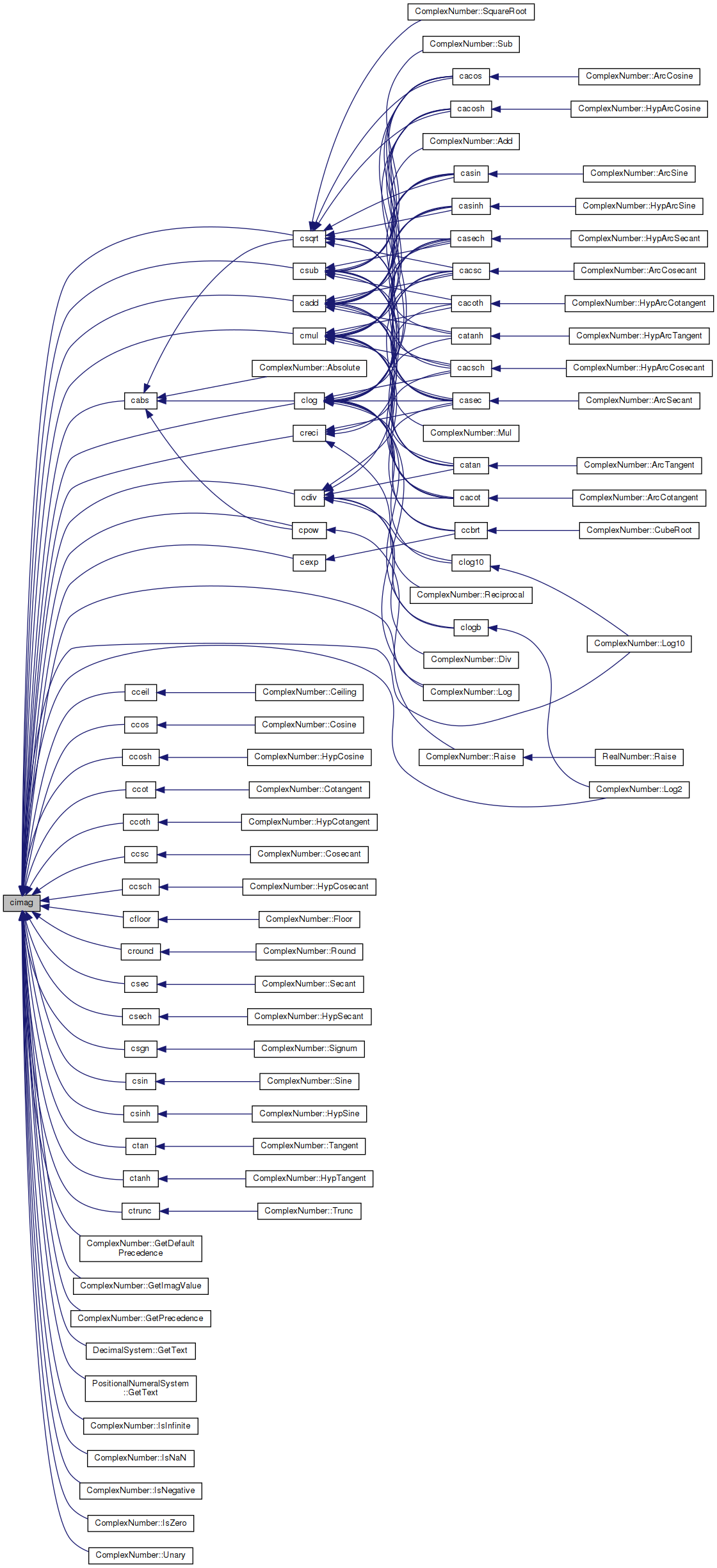
Imaginary part of complex number.

Definition at line 46 of file prim.c.

Referenced by cabs(), cadd(), cceil(), ccos(), ccosh(), ccot(), ccoth(), ccsc(), ccsch(), cdiv(), cexp(), cfloor(), clog(), cmul(), cpow(), creci(), cround(), csec(), csech(), csgn(), csin(), csinh(), csqrt(), csub(), ctan(), ctanh(), ctrunc(), ComplexNumber::GetDefaultPrecedence(), ComplexNumber::GetImagValue(), ComplexNumber::GetPrecedence(), DecimalSystem::GetText(), PositionalNumeralSystem::GetText(), ComplexNumber::IsInfinite(), ComplexNumber::IsNaN(), ComplexNumber::IsNegative(), ComplexNumber::IsZero(), ComplexNumber::Log(), ComplexNumber::Log10(), ComplexNumber::Log2(), and ComplexNumber::Unary().

{
    return (IMAG_PART(z));
}

Here is the caller graph for this function:

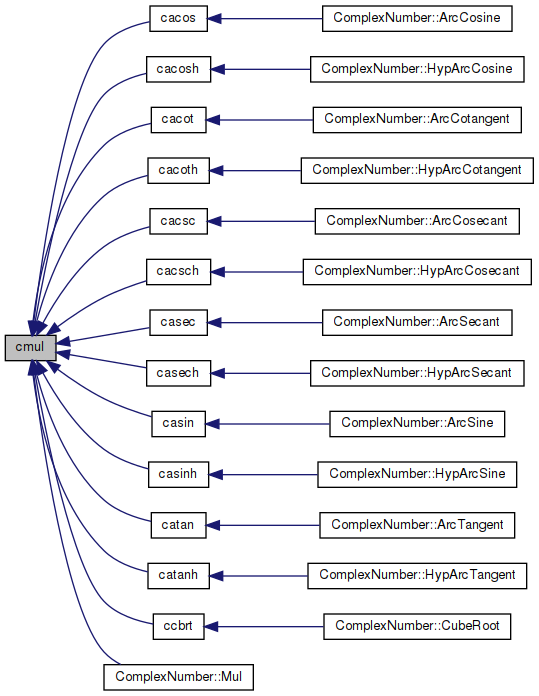
cmul()

complex cmul	(	complex	y,
		complex	z
	)

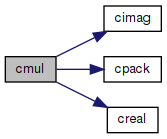
Multiplication of two complex numbers.

Definition at line 140 of file prim.c.

References cimag(), cpack(), and creal().

Referenced by cacos(), cacosh(), cacot(), cacoth(), cacsc(), cacsch(), casec(), casech(), casin(), casinh(), catan(), catanh(), ccbrt(), and ComplexNumber::Mul().

{
    complex w;
    double a, b, c, d;

    // (a+bi)(c+di)
    a = creal(y);
    b = cimag(y);
    c = creal(z);
    d = cimag(z);

    // (ac -bd) + (ad + bc)i
    w = cpack(a * c - b * d, a * d + b * c);
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

conj()

complex conj

(

complex

z

)

Definition at line 59 of file prim.c.

References cpack().

Referenced by creci().

{
    IMAG_PART(z) = -IMAG_PART(z);
    return cpack(REAL_PART(z), IMAG_PART(z));
}

Here is the call graph for this function:

Here is the caller graph for this function:

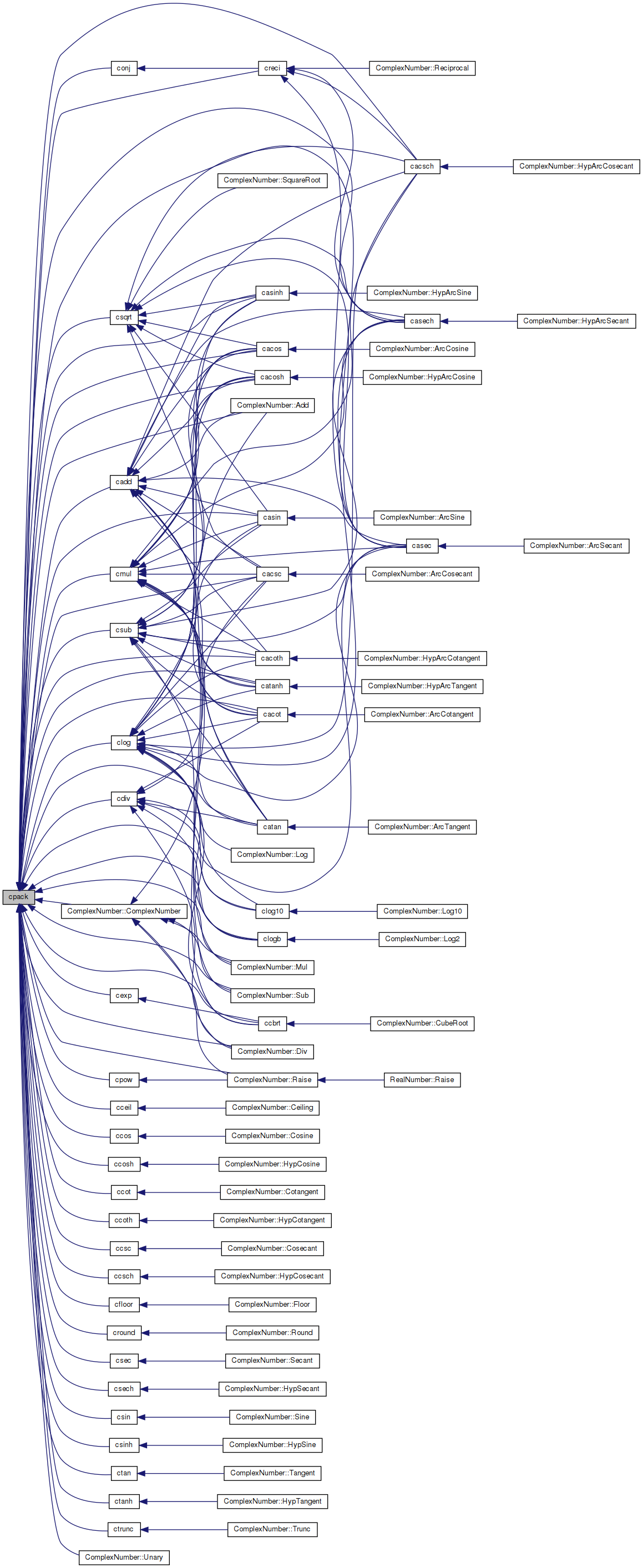
cpack()

complex cpack	(	double	x,
		double	y
	)

Pack two real numbers into a complex number.

Definition at line 68 of file prim.c.

Referenced by ComplexNumber::Add(), cacos(), cacosh(), cacot(), cacoth(), cacsc(), cacsch(), cadd(), casec(), casech(), casin(), casinh(), catan(), catanh(), ccbrt(), cceil(), ccos(), ccosh(), ccot(), ccoth(), ccsc(), ccsch(), cdiv(), cexp(), cfloor(), clog(), clog10(), clogb(), cmul(), ComplexNumber::ComplexNumber(), conj(), cpow(), creci(), cround(), csec(), csech(), csin(), csinh(), csqrt(), csub(), ctan(), ctanh(), ctrunc(), ComplexNumber::Div(), ComplexNumber::Mul(), ComplexNumber::Raise(), ComplexNumber::Sub(), and ComplexNumber::Unary().

{
    complex z;

    REAL_PART(z) = x;
    IMAG_PART(z) = y;
    return (z);
}

Here is the caller graph for this function:

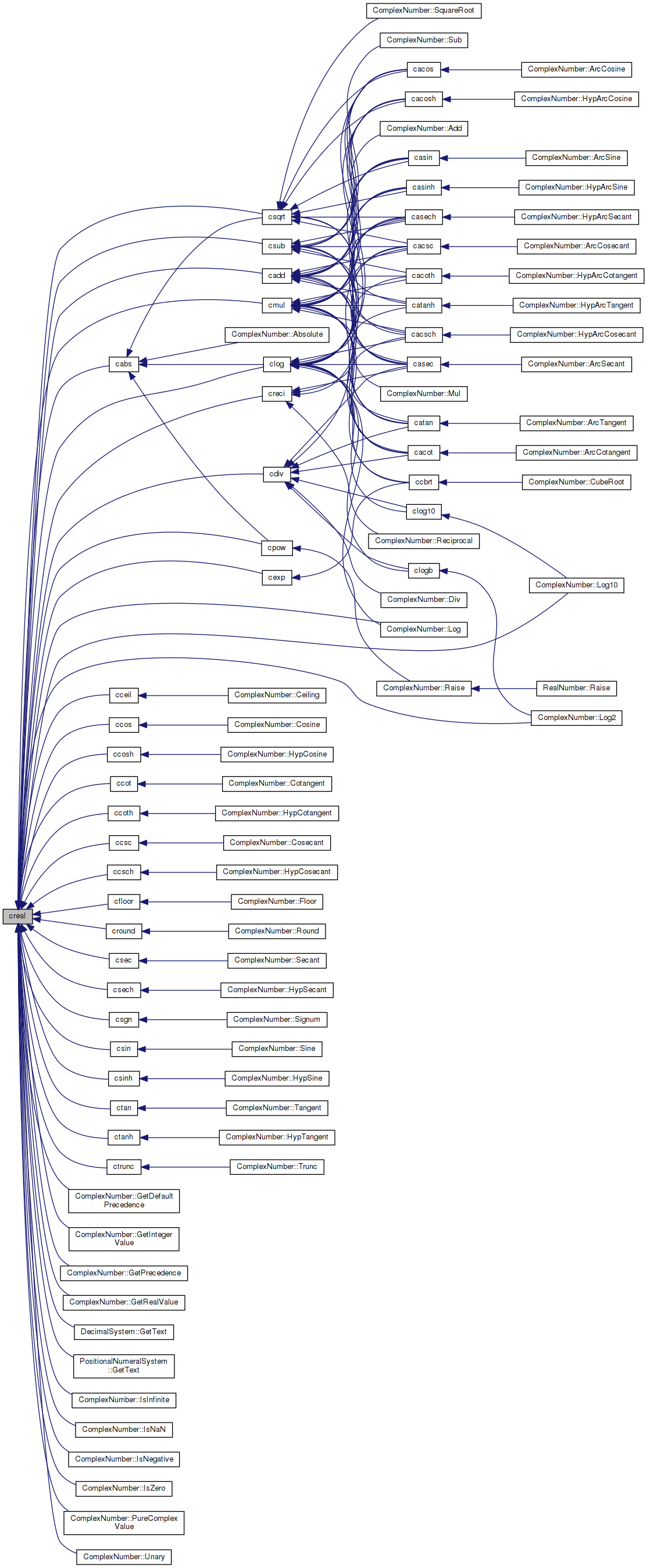
creal()

double creal

(

complex

z

)

Real part of complex number.

Definition at line 38 of file prim.c.

Referenced by cabs(), cadd(), cceil(), ccos(), ccosh(), ccot(), ccoth(), ccsc(), ccsch(), cdiv(), cexp(), cfloor(), clog(), cmul(), cpow(), creci(), cround(), csec(), csech(), csgn(), csin(), csinh(), csqrt(), csub(), ctan(), ctanh(), ctrunc(), ComplexNumber::GetDefaultPrecedence(), ComplexNumber::GetIntegerValue(), ComplexNumber::GetPrecedence(), ComplexNumber::GetRealValue(), DecimalSystem::GetText(), PositionalNumeralSystem::GetText(), ComplexNumber::IsInfinite(), ComplexNumber::IsNaN(), ComplexNumber::IsNegative(), ComplexNumber::IsZero(), ComplexNumber::Log(), ComplexNumber::Log10(), ComplexNumber::Log2(), ComplexNumber::PureComplexValue(), and ComplexNumber::Unary().

{
    return (REAL_PART(z));
}

Here is the caller graph for this function:

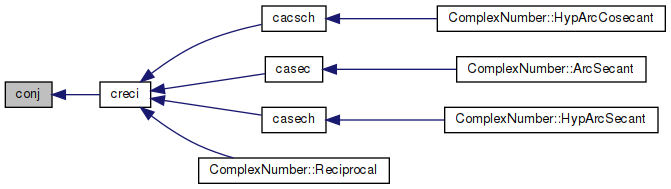
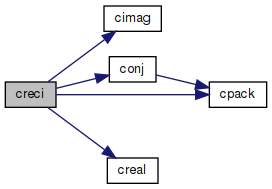
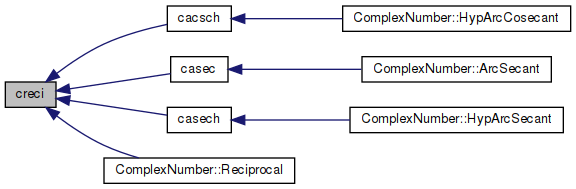
creci()

complex creci

(

complex

z

)

Reciprocal value of complex number.

Definition at line 181 of file prim.c.

References cimag(), conj(), cpack(), and creal().

Referenced by cacsch(), casec(), casech(), and ComplexNumber::Reciprocal().

{
    complex w;
    double q, a, b;

    a = creal(z);
    b = cimag(conj(z));
    q = a * a + b * b;
    w = cpack(a / q, b / q);

    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

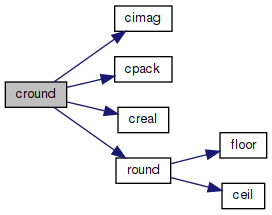
cround()

complex cround

(

complex

z

)

Division of two complex numbers.

Definition at line 110 of file prim.c.

References cimag(), cpack(), creal(), and round().

Referenced by ComplexNumber::Round().

{
    complex w;
    w = cpack(round(creal(z)), round(cimag(z)));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

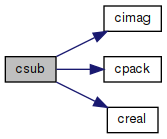
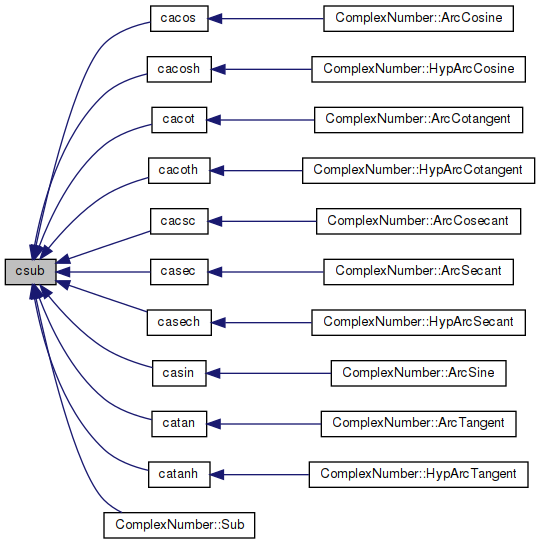
csub()

complex csub	(	complex	y,
		complex	z
	)

Subtraction of two complex numbers.

Definition at line 130 of file prim.c.

References cimag(), cpack(), and creal().

Referenced by cacos(), cacosh(), cacot(), cacoth(), cacsc(), casec(), casech(), casin(), catan(), catanh(), and ComplexNumber::Sub().

{
    complex w;
    w = cpack(creal(y) - creal(z), cimag(y) - cimag(z));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

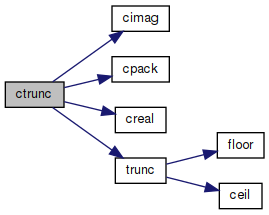
ctrunc()

complex ctrunc

(

complex

z

)

Truncated value of complex number.

Definition at line 80 of file prim.c.

References cimag(), cpack(), creal(), and trunc().

Referenced by ComplexNumber::Trunc().

{
    complex w;
    w = cpack(trunc(creal(z)), trunc(cimag(z)));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function: