hypot.c File Reference

#include "prim.h"

Include dependency graph for hypot.c:

Go to the source code of this file.

Functions
double	hypot (double x, double y)
	hypot More...

Function Documentation

hypot()

double hypot	(	double	x,
		double	y
	)

hypot

Method
 If (assume round-to-nearest) z=x*x+y*y
 has error less than sqrt(2)/2 ulp, than
 sqrt(z) has error less than 1 ulp (exercise).

 So, compute sqrt(x*x+y*y) with some care as
 follows to get the error below 1 ulp:

 Assume x>y>0;
 (if possible, set rounding to round-to-nearest)
 1. if x > 2y  use
    x1*x1+(y*y+(x2*(x+x1))) for x*x+y*y
 where x1 = x with lower 32 bits cleared, x2 = x-x1; else
 2. if x <= 2y use
    t1*y1+((x-y)*(x-y)+(t1*y2+t2*y))
 where t1 = 2x with lower 32 bits cleared, t2 = 2x-t1,
 y1= y with lower 32 bits chopped, y2 = y-y1.

 NOTE: scaling may be necessary if some argument is too
       large or too tiny

Special cases:
 hypot(x,y) is INF if x or y is +INF or -INF; else
 hypot(x,y) is NAN if x or y is NAN.

Accuracy:
    hypot(x,y) returns sqrt(x^2+y^2) with error less
    than 1 ulps (units in the last place)

Definition at line 81 of file hypot.c.

References sqrt().

Referenced by cabs().

{
    double a = x, b = y, t1, t2, y1, y2, w;
    uint32_t j, k, ha, hb, hx, hy;

    GET_HIGH_WORD(hx, x);
    GET_HIGH_WORD(hy, y);
    ha = hx & 0x7FFFFFFF; // high word of x
    hb = hy & 0x7FFFFFFF; // high word of y

    if (hb > ha)
    {
        a = y;
        b = x;
        j = ha;
        ha = hb;
        hb = j;
    }
    else
    {
        a = x;
        b = y;
    }

    SET_HIGH_WORD(a, ha); // a <- |a|
    SET_HIGH_WORD(b, hb); // b <- |b|

    // x/y > 2**60
    if ((ha - hb) > 0x3C00000)
    {
        return a + b;
    }

    k = 0;

    // a>2**500
    if (ha > 0x5F300000)
    {
        // Inf or NaN
        if (ha >= 0x7FF00000)
        {
            uint32_t la, lb;
            w = a + b; // for sNaN
            GET_LOW_WORD(la, a);
            GET_LOW_WORD(lb, b);

            if (((ha & 0xFFFFF) | la) == 0)
            {
                w = a;
            }

            if (((hb ^ 0x7FF00000) | lb) == 0)
            {
                w = b;
            }

            return w;
        }

        // scale a and b by 2**-600
        ha -= 0x25800000;
        hb -= 0x25800000;
        k += 600;
        SET_HIGH_WORD(a, ha);
        SET_HIGH_WORD(b, hb);
    }

    // b < 2**-500
    if (hb < 0x20B00000)
    {
        // subnormal b or 0
        if (hb <= 0x000FFFFF)
        {
            uint32_t lb;
            GET_LOW_WORD(lb, b);
            if ((hb | lb) == 0)
            {
                return a;
            }

            t1 = 0;
            SET_HIGH_WORD(t1, 0x7FD00000); /* t1=2^1022 */
            b *= t1;
            a *= t1;
            k -= 1022;
        }
        else
        {                     /* scale a and b by 2^600 */
            ha += 0x25800000; /* a *= 2^600 */
            hb += 0x25800000; /* b *= 2^600 */
            k -= 600;

            SET_HIGH_WORD(a, ha);
            SET_HIGH_WORD(b, hb);
        }
    }

    // medium size a and b
    w = a - b;
    if (w > b)
    {
        t1 = 0;
        SET_HIGH_WORD(t1, ha);
        t2 = a - t1;
        w = sqrt(t1 * t1 - (b * (-b) - t2 * (a + t1)));
    }
    else
    {
        a = a + a;
        y1 = 0;
        SET_HIGH_WORD(y1, hb);
        y2 = b - y1;
        t1 = 0;
        SET_HIGH_WORD(t1, ha + 0x00100000);
        t2 = a - t1;
        w = sqrt(t1 * y1 - (w * (-w) - (t1 * y2 + t2 * b)));
    }

    if (k != 0)
    {
        uint32_t ht1;
        t1 = 1.0;
        GET_HIGH_WORD(ht1, t1);
        SET_HIGH_WORD(t1, ht1 + (k << 20));
        return t1 * w;
    }

    return w;
}

Here is the call graph for this function:

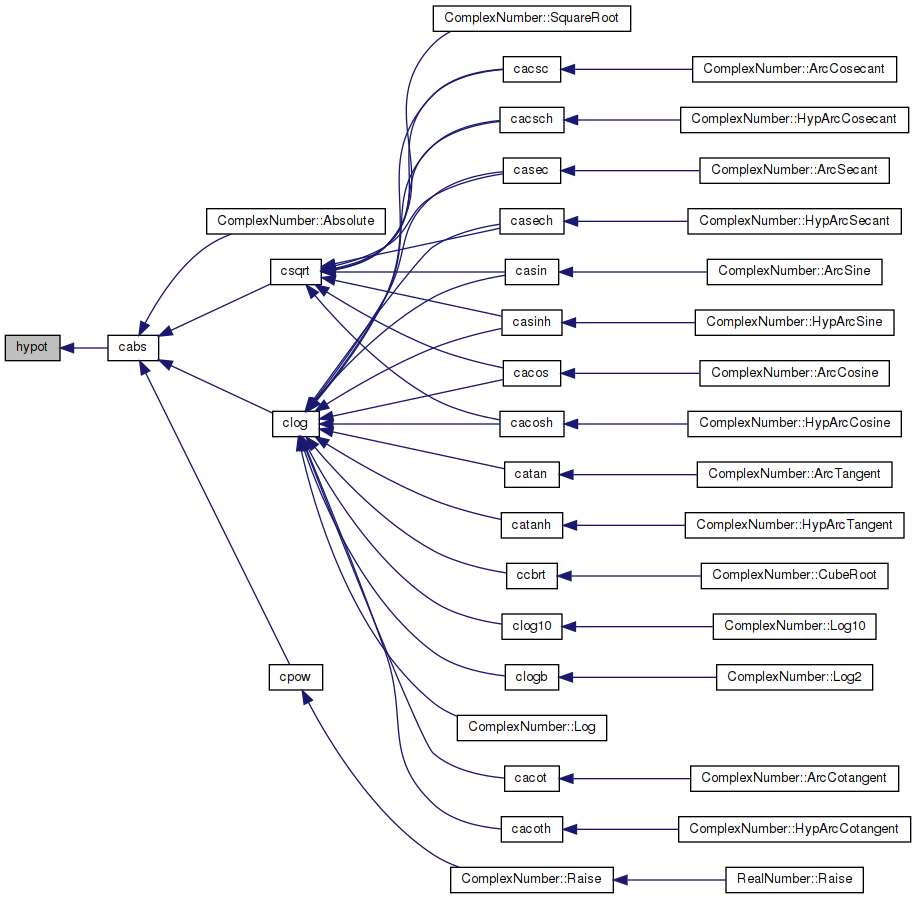
Here is the caller graph for this function: