mathi.h File Reference

Complex numbers math library. More...

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Classes
union	complex

Functions
double	csgn (complex z)
	Complex signum. More...
double	cabs (complex z)
	Absolute value of complex number. More...
double	creal (complex z)
	Real part of complex number. More...
double	cimag (complex z)
	Imaginary part of complex number. More...
complex	cpack (double x, double y)
	Pack two real numbers into a complex number. More...
complex	cadd (complex a, complex z)
	Addition of two complex numbers. More...
complex	csub (complex a, complex z)
	Subtraction of two complex numbers. More...
complex	cmul (complex a, complex z)
	Multiplication of two complex numbers. More...
complex	cdiv (complex a, complex z)
	Division of two complex numbers. More...
complex	cpow (complex x, complex z)
	Complex number raised to a power. More...
complex	cceil (complex z)
	Ceiling value of complex number. More...
complex	cfloor (complex z)
	Floor value of complex number. More...
complex	ctrunc (complex z)
	Truncated value of complex number. More...
complex	cround (complex z)
	Division of two complex numbers. More...
complex	creci (complex z)
	Reciprocal value of complex number. More...
complex	conj (complex z)
complex	cexp (complex z)
	Returns e to the power of a complex number. More...
complex	csqrt (complex z)
	Square root of complex number. More...
complex	ccbrt (complex z)
	Cube root of complex number. More...
complex	clog (complex z)
	Natural logarithm of a complex number. More...
complex	clogb (complex z)
	Base 2 logarithmic value of complex number. More...
complex	clog10 (complex z)
	Base 10 logarithmic value of complex number. More...
complex	ccos (complex z)
	Cosine of complex number. More...
complex	csin (complex z)
	Sine of a complex number. More...
complex	ctan (complex z)
	Tangent of a complex number. More...
complex	csec (complex z)
	Secant of a complex number. More...
complex	ccsc (complex z)
	Cosecant of a complex number. More...
complex	ccot (complex z)
	Cotangent of a complex number. More...
complex	cacos (complex z)
	Inverse cosine of complex number. More...
complex	casin (complex z)
	Inverse sine of complex number. More...
complex	catan (complex z)
	Inverse tangent of complex number. More...
complex	casec (complex z)
	Inverse secant expressed using complex logarithms: More...
complex	cacsc (complex z)
	Inverse cosecant of complex number. More...
complex	cacot (complex z)
	Inverse cotangent of complex number. More...
complex	ccosh (complex z)
	Hyperbolic cosine of a complex number. More...
complex	csinh (complex z)
	Hyperbolic sine of a complex number. More...
complex	ctanh (complex z)
	Hyperbolic tangent of a complex number. More...
complex	csech (complex z)
	Hyperbolic secant of a complex number. More...
complex	ccsch (complex z)
	Hyperbolic secant of a complex number. More...
complex	ccoth (complex z)
	Hyperbolic cotangent of a complex number. More...
complex	cacosh (complex z)
	Inverse hyperbolic cosine of complex number. More...
complex	casinh (complex z)
	Inverse hyperbolic sine of complex number. More...
complex	catanh (complex z)
	Inverse hyperbolic tangent of complex number. More...
complex	casech (complex z)
	Inverse hyperbolic secant of complex numbers. More...
complex	cacsch (complex z)
	Inverse hyperbolic cosecant of complex number. More...
complex	cacoth (complex z)
	Inverse hyperbolic cotangent of complex number. More...

Detailed Description

Complex numbers math library.

Mostly as specified in [IEEE Std 1003.1, 2013 Edition]: http://pubs.opengroup.org/onlinepubs/9699919799/basedefs/complex.h.html

Definition in file mathi.h.

Function Documentation

cabs()

double cabs

(

complex

z

)

Absolute value of complex number.

Definition at line 54 of file prim.c.

References cimag(), creal(), and hypot().

Referenced by ComplexNumber::Absolute(), clog(), cpow(), and csqrt().

{
    return hypot(creal(z), cimag(z));
}

Here is the call graph for this function:

Here is the caller graph for this function:

cacos()

complex cacos

(

complex

z

)

Inverse cosine of complex number.

Inverse cosine expressed using complex logarithms:

arccos z = -i * log(z + i * sqrt(1 - z * z))

More info is available at Wikipedia:
https://wikipedia.org/wiki/Inverse_trigonometric_functions#Logarithmic_forms

Definition at line 42 of file cacos.c.

References cadd(), clog(), cmul(), cpack(), csqrt(), and csub().

Referenced by ComplexNumber::ArcCosine().

{
    complex a = cpack(1.0, 0.0);
    complex i = cpack(0.0, 1.0);
    complex j = cpack(0.0, -1.0);
    complex p = csub(a, cmul(z, z));
    complex q = clog(cadd(z, cmul(i, csqrt(p))));
    complex w = cmul(j, q);
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cacosh()

complex cacosh

(

complex

z

)

Inverse hyperbolic cosine of complex number.

Inverse hyperbolic cosine expressed using complex logarithms:

acosh(z) = log(z + sqrt(z*z - 1))

More info is available at Wikipedia:
https://wikipedia.org/wiki/Inverse_hyperbolic_function#Logarithmic_representation

Definition at line 42 of file cacosh.c.

References cadd(), clog(), cmul(), cpack(), csqrt(), and csub().

Referenced by ComplexNumber::HypArcCosine().

{
    complex one = cpack(1.0, 0.0);
    complex a = csub(cmul(z, z), one);
    complex b = cadd(z, csqrt(a));
    complex w = clog(b);
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cacot()

complex cacot

(

complex

z

)

Inverse cotangent of complex number.

Inverse cotangent expressed using complex logarithms:

arccot z = i/2 * (log(1 - i/z) - log(1 + i/z))

More info is available at Wikipedia:
https://wikipedia.org/wiki/Inverse_trigonometric_functions#Logarithmic_forms

Definition at line 42 of file cacot.c.

References cadd(), cdiv(), clog(), cmul(), cpack(), and csub().

Referenced by ComplexNumber::ArcCotangent().

{
    complex one = cpack(1.0, 0.0);
    complex two = cpack(2.0, 0.0);
    complex i = cpack(0.0, 1.0);
    complex iz = cdiv(i, z);
    complex p = clog(csub(one, iz));
    complex q = clog(cadd(one, iz));
    complex w = cmul(cdiv(i, two), csub(p, q));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cacoth()

complex cacoth

(

complex

z

)

Inverse hyperbolic cotangent of complex number.

Inverse hyperbolic cotangent expressed using complex logarithms:

acoth(z) = 1/2 * ((log(z + 1) - log(z - 1))

More info is available at Wikipedia:
https://wikipedia.org/wiki/Inverse_hyperbolic_function#Logarithmic_representation

Definition at line 42 of file cacoth.c.

References cadd(), clog(), cmul(), cpack(), and csub().

Referenced by ComplexNumber::HypArcCotangent().

{
    complex half = cpack(0.5, 0.0);
    complex one = cpack(1.0, 0.0);
    complex a = clog(cadd(z, one));
    complex b = clog(csub(z, one));
    complex c = csub(a, b);
    complex w = cmul(half, c);
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cacsc()

complex cacsc

(

complex

z

)

Inverse cosecant of complex number.

Inverse cosecant expressed using complex logarithms:

arccsc z = -i * log(sqr(1 - 1/(z*z)) + i/z)

More info is available at Wikipedia:
https://wikipedia.org/wiki/Inverse_trigonometric_functions#Logarithmic_forms

Definition at line 42 of file cacsc.c.

References cadd(), cdiv(), clog(), cmul(), cpack(), csqrt(), and csub().

Referenced by ComplexNumber::ArcCosecant().

{
    complex one = cpack(1.0, 0.0);
    complex i = cpack(0.0, 1.0);
    complex j = cpack(0.0, -1.0);
    complex iz = cdiv(i, z);
    complex z2 = cmul(z, z);
    complex p = cdiv(one, z2);
    complex q = csqrt(csub(one, p));
    complex w = cmul(j, clog(cadd(q, iz)));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cacsch()

complex cacsch

(

complex

z

)

Inverse hyperbolic cosecant of complex number.

Inverse hyperbolic cosecant expressed using complex logarithms:

acsch(z) = log(sqrt(1 + 1 / (z * z)) + 1/z)

More info is available at Wikipedia:
https://wikipedia.org/wiki/Inverse_hyperbolic_function#Logarithmic_representation

Definition at line 42 of file cacsch.c.

References cadd(), clog(), cmul(), cpack(), creci(), and csqrt().

Referenced by ComplexNumber::HypArcCosecant().

{
    complex one = cpack(1.0, 0.0);
    complex a = creci(cmul(z, z));
    complex b = csqrt(cadd(one, a));
    complex c = cadd(b, creci(z));
    complex w = clog(c);
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cadd()

complex cadd	(	complex	a,
		complex	z
	)

Addition of two complex numbers.

Definition at line 120 of file prim.c.

References cimag(), cpack(), and creal().

Referenced by ComplexNumber::Add(), cacos(), cacosh(), cacot(), cacoth(), cacsc(), cacsch(), casec(), casech(), casin(), casinh(), catan(), and catanh().

{
    complex w;
    w = cpack(creal(y) + creal(z), cimag(y) + cimag(z));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

casec()

complex casec

(

complex

z

)

Inverse secant expressed using complex logarithms:

Inverse secant expressed using complex logarithms:

arcsec z = -i * log(i * sqr(1 - 1/(z*z)) + 1/z)

More info is available at Wikipedia:
https://wikipedia.org/wiki/Inverse_trigonometric_functions#Logarithmic_forms

Definition at line 42 of file casec.c.

References cadd(), cdiv(), clog(), cmul(), cpack(), creci(), csqrt(), and csub().

Referenced by ComplexNumber::ArcSecant().

{
    complex one = cpack(1.0, 0.0);
    complex i = cpack(0.0, 1.0);
    complex j = cpack(0.0, -1.0);
    complex rz = creci(z);
    complex z2 = cmul(z, z);
    complex p = cdiv(one, z2);
    complex q = csqrt(csub(one, p));
    complex w = cmul(j, clog(cadd(cmul(i, q), rz)));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

casech()

complex casech

(

complex

z

)

Inverse hyperbolic secant of complex numbers.

Inverse hyperbolic secant expressed using complex logarithms:

asech(z) = log(sqrt(1 / (z * z) - 1) + 1/z)

More info is available at Wikipedia:
https://wikipedia.org/wiki/Inverse_hyperbolic_function#Logarithmic_representation

Definition at line 42 of file casech.c.

References cadd(), clog(), cmul(), cpack(), creci(), csqrt(), and csub().

Referenced by ComplexNumber::HypArcSecant().

{
    complex one = cpack(1.0, 0.0);
    complex a = creci(cmul(z, z));
    complex b = csqrt(csub(a, one));
    complex c = cadd(b, creci(z));
    complex w = clog(c);
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

casin()

complex casin

(

complex

z

)

Inverse sine of complex number.

Inverse sine expressed using complex logarithms:

arcsin z = -i * log(iz + sqrt(1 - z*z))

More info is available at Wikipedia:
https://wikipedia.org/wiki/Inverse_trigonometric_functions#Logarithmic_forms

Definition at line 42 of file casin.c.

References cadd(), clog(), cmul(), cpack(), csqrt(), and csub().

Referenced by ComplexNumber::ArcSine().

{
    complex one = cpack(1.0, 0.0);
    complex i = cpack(0.0, 1.0);
    complex j = cpack(0.0, -1.0);
    complex iz = cmul(i, z);
    complex z2 = cmul(z, z);
    complex p = csqrt(csub(one, z2));
    complex q = clog(cadd(iz, p));
    complex w = cmul(j, q);
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

casinh()

complex casinh

(

complex

z

)

Inverse hyperbolic sine of complex number.

Inverse hyperbolic sine expressed using complex logarithms:

asinh(z) = log(z + sqrt(z*z + 1))

With branch cuts: -i INF to -i and i to i INF

Domain: -INF to INF
Range:  -INF to INF

More info is available at Wikipedia:
https://wikipedia.org/wiki/Inverse_hyperbolic_function#Logarithmic_representation

Definition at line 47 of file casinh.c.

References cadd(), clog(), cmul(), cpack(), and csqrt().

Referenced by ComplexNumber::HypArcSine().

{
    // TODO: Fix branch cuts
    complex one = cpack(1.0, 0.0);
    complex a = cadd(cmul(z, z), one);
    complex b = cadd(z, csqrt(a));
    complex w = clog(b);
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

catan()

complex catan

(

complex

z

)

Inverse tangent of complex number.

Inverse tangent expressed using complex logarithms:

atan(z) = i/2 * (log(1 - i * z) - log(1 + i * z))

More info is available at Wikipedia:
https://wikipedia.org/wiki/Inverse_trigonometric_functions#Logarithmic_forms

Definition at line 42 of file catan.c.

References cadd(), cdiv(), clog(), cmul(), cpack(), and csub().

Referenced by ComplexNumber::ArcTangent().

{
    complex one = cpack(1.0, 0.0);
    complex two = cpack(2.0, 0.0);
    complex i = cpack(0.0, 1.0);
    complex iz = cmul(i, z);
    complex p = clog(csub(one, iz));
    complex q = clog(cadd(one, iz));
    complex w = cmul(cdiv(i, two), csub(p, q));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

catanh()

complex catanh

(

complex

z

)

Inverse hyperbolic tangent of complex number.

Inverse hyperbolic tangent expressed using complex logarithms:

atanh(z) = 1/2 * ((log(1 + z) - log(1 - z))

More info is available at Wikipedia:
https://wikipedia.org/wiki/Inverse_hyperbolic_function#Logarithmic_representation

Definition at line 42 of file catanh.c.

References cadd(), clog(), cmul(), cpack(), and csub().

Referenced by ComplexNumber::HypArcTangent().

{
    complex half = cpack(0.5, 0.0);
    complex one = cpack(1.0, 0.0);
    complex a = clog(cadd(one, z));
    complex b = clog(csub(one, z));
    complex c = csub(a, b);
    complex w = cmul(half, c);
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

ccbrt()

complex ccbrt

(

complex

z

)

Cube root of complex number.

cbrt z = exp(1/3 * log(z))

More info is available at Wikipedia:
https://wikipedia.org/wiki/Cube_root

Definition at line 41 of file ccbrt.c.

References cexp(), clog(), cmul(), and cpack().

Referenced by ComplexNumber::CubeRoot().

{
    complex onethird = cpack(1.0 / 3.0, 0.0);
    complex a = cmul(onethird, clog(z));
    complex w = cexp(a);
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cceil()

complex cceil

(

complex

z

)

Ceiling value of complex number.

Definition at line 100 of file prim.c.

References ceil(), cimag(), cpack(), and creal().

Referenced by ComplexNumber::Ceiling().

{
    complex w;
    w = cpack(ceil(creal(z)), ceil(cimag(z)));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

ccos()

complex ccos

(

complex

z

)

Cosine of complex number.

a+bi
real =  cos(a) * cosh(b)
imag = -sin(a) * sinh(b)

Definition at line 45 of file ccos.c.

References cchsh(), cimag(), cos(), cpack(), creal(), and sin().

Referenced by ComplexNumber::Cosine().

{
    complex w;
    double a, b;
    double ch, sh;

    a = creal(z);
    b = cimag(z);
    cchsh(b, &ch, &sh);
    w = cpack((cos(a) * ch), (-sin(a) * sh));

    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

ccosh()

complex ccosh

(

complex

z

)

Hyperbolic cosine of a complex number.

a+bi
real = cosh(a) * cos(b)
imag = sinh(a) * sin(b)

Definition at line 48 of file ccosh.c.

References cchsh(), cimag(), cos(), cpack(), creal(), and sin().

Referenced by ComplexNumber::HypCosine().

{
    complex w;
    double a, b;
    double ch, sh;

    a = creal(z);
    b = cimag(z);
    cchsh(a, &ch, &sh);
    w = cpack(cos(b) * ch, sin(b) * sh);

    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

ccot()

complex ccot

(

complex

z

)

Cotangent of a complex number.

Calculated as in Open Office:

a+bi
                sin(2.0 * a)
real  = ------------------------------
         cosh(2.0 * b) - cos(2.0 * a)

               -sinh(2.0 * b)
imag  = ------------------------------
         cosh(2.0 * b) - cos(2.0 * a)

https://wiki.openoffice.org/wiki/Documentation/How_Tos/Calc:_IMCOT_function

Definition at line 48 of file ccot.c.

References cimag(), cos(), cosh(), cpack(), creal(), sin(), and sinh().

Referenced by ComplexNumber::Cotangent().

{
    complex w;
    double a, b;
    double d;

    a = creal(z);
    b = cimag(z);
    d = cosh(2.0 * b) - cos(2.0 * a);

    if (d == 0.0)
    {
        w = cpack((double)INFP, (double)INFP);
    }
    else
    {
        w = cpack((sin(2.0 * a) / d), (-sinh(2.0 * b) / d));
    }

    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

ccoth()

complex ccoth

(

complex

z

)

Hyperbolic cotangent of a complex number.

acoth(z) = 0.5 * (log(1 + 1/z) - log(1 - 1/z))

or

a+bi
               sinh(2.0 * a)
real  = ---------------------------—
         cosh(2.0 * a) - cos(2.0 * b)
  -sin(2.0 * b)

imag  = ---------------------------—
         cosh(2.0 * a) - cos(2.0 * b)

Definition at line 50 of file ccoth.c.

References cimag(), cos(), cosh(), cpack(), creal(), sin(), and sinh().

Referenced by ComplexNumber::HypCotangent().

{
    complex w;
    double a, b;
    double d;

    a = creal(z);
    b = cimag(z);
    d = cosh(2.0 * a) - cos(2.0 * b);
    w = cpack(sinh(2.0 * a) / d, -sin(2.0 * b) / d);

    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

ccsc()

complex ccsc

(

complex

z

)

Cosecant of a complex number.

Calculated as in Open Office:

a+bi
            2.0 * sin(a) * cosh(b)
real  = ------------------------------
         cosh(2.0 * b) - cos(2.0 * a)

           -2.0 * cos(a) * sinh(b)
imag  = ------------------------------
         cosh(2.0 * b) - cos(2.0 * a)

https://wiki.openoffice.org/wiki/Documentation/How_Tos/Calc:_IMCSC_function

Definition at line 48 of file ccsc.c.

References cimag(), cos(), cosh(), cpack(), creal(), sin(), and sinh().

Referenced by ComplexNumber::Cosecant().

{
    complex w;
    double a, b;
    double d;

    a = creal(z);
    b = cimag(z);
    d = cosh(2.0 * b) - cos(2.0 * a);

    if (d == 0.0)
    {
        w = cpack((double)INFP, (double)INFP);
    }
    else
    {
        w = cpack((2.0 * sin(a) * cosh(b) / d), (-2.0 * cos(a) * sinh(b) / d));
    }

    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

ccsch()

complex ccsch

(

complex

z

)

Hyperbolic secant of a complex number.

Calculated as in Open Office:

a+bi
            2.0 * sinh(a) * cos(b)
real  = ------------------------------
         cosh(2.0 * a) - cos(2.0 * b)

        -2.0 * cosh(2.0 * a) * sin(b)
imag  = ------------------------------
         cosh(2.0 * a) - cos(2.0 * b)

https://wiki.openoffice.org/wiki/Documentation/How_Tos/Calc:_IMCSCH_function

Definition at line 48 of file ccsch.c.

References cimag(), cos(), cosh(), cpack(), creal(), sin(), and sinh().

Referenced by ComplexNumber::HypCosecant().

{
    complex w;
    double a, b;
    double d;

    a = creal(z);
    b = cimag(z);
    d = cosh(2.0 * a) - cos(2.0 * b);
    w = cpack((2.0 * sinh(a) * cos(b) / d), (-2.0 * cosh(a) * sin(b) / d));

    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cdiv()

complex cdiv	(	complex	a,
		complex	z
	)

Division of two complex numbers.

Definition at line 159 of file prim.c.

References cimag(), cpack(), and creal().

Referenced by cacot(), cacsc(), casec(), catan(), clog10(), clogb(), and ComplexNumber::Div().

{
    complex w;
    double a, b, c, d;
    double q, v, x;

    a = creal(y);
    b = cimag(y);
    c = creal(z);
    d = cimag(z);

    q = c * c + d * d;
    v = a * c + b * d;
    x = b * c - a * d;

    w = cpack(v / q, x / q);
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cexp()

complex cexp

(

complex

z

)

Returns e to the power of a complex number.

Definition at line 42 of file cexp.c.

References cimag(), cos(), cpack(), creal(), exp(), and sin().

Referenced by ccbrt().

{
    complex w;
    double r, x, y;
    x = creal(z);
    y = cimag(z);
    r = exp(x);
    w = cpack(r * cos(y), r * sin(y));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cfloor()

complex cfloor

(

complex

z

)

Floor value of complex number.

Definition at line 90 of file prim.c.

References cimag(), cpack(), creal(), and floor().

Referenced by ComplexNumber::Floor().

{
    complex w;
    w = cpack(floor(creal(z)), floor(cimag(z)));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cimag()

double cimag

(

complex

z

)

Imaginary part of complex number.

Definition at line 46 of file prim.c.

Referenced by cabs(), cadd(), cceil(), ccos(), ccosh(), ccot(), ccoth(), ccsc(), ccsch(), cdiv(), cexp(), cfloor(), clog(), cmul(), cpow(), creci(), cround(), csec(), csech(), csgn(), csin(), csinh(), csqrt(), csub(), ctan(), ctanh(), ctrunc(), ComplexNumber::GetDefaultPrecedence(), ComplexNumber::GetImagValue(), ComplexNumber::GetPrecedence(), DecimalSystem::GetText(), PositionalNumeralSystem::GetText(), ComplexNumber::IsInfinite(), ComplexNumber::IsNaN(), ComplexNumber::IsNegative(), ComplexNumber::IsZero(), ComplexNumber::Log(), ComplexNumber::Log10(), ComplexNumber::Log2(), and ComplexNumber::Unary().

{
    return (IMAG_PART(z));
}

Here is the caller graph for this function:

clog()

complex clog

(

complex

z

)

Natural logarithm of a complex number.

Definition at line 42 of file clog.c.

References atan2(), cabs(), cimag(), cpack(), creal(), and log().

Referenced by cacos(), cacosh(), cacot(), cacoth(), cacsc(), cacsch(), casec(), casech(), casin(), casinh(), catan(), catanh(), ccbrt(), clog10(), clogb(), and ComplexNumber::Log().

{
    complex w;
    double p, q;
    p = log(cabs(z));
    q = atan2(cimag(z), creal(z));
    w = cpack(p, q);
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

clog10()

complex clog10

(

complex

z

)

Base 10 logarithmic value of complex number.

log z = log(z) / log(10)

More info is available at Wikipedia:
https://wikipedia.org/wiki/Complex_logarithm

Definition at line 41 of file clog10.c.

References cdiv(), clog(), and cpack().

Referenced by ComplexNumber::Log10().

{
    complex teen = cpack(10.0, 0.0);
    complex w = cdiv(clog(z), clog(teen));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

clogb()

complex clogb

(

complex

z

)

Base 2 logarithmic value of complex number.

lb z = log(z) / log(2)

More info is available at Wikipedia:
https://wikipedia.org/wiki/Complex_logarithm

Definition at line 41 of file clogb.c.

References cdiv(), clog(), and cpack().

Referenced by ComplexNumber::Log2().

{
    complex two = cpack(2.0, 0.0);
    complex w = cdiv(clog(z), clog(two));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cmul()

complex cmul	(	complex	a,
		complex	z
	)

Multiplication of two complex numbers.

Definition at line 140 of file prim.c.

References cimag(), cpack(), and creal().

Referenced by cacos(), cacosh(), cacot(), cacoth(), cacsc(), cacsch(), casec(), casech(), casin(), casinh(), catan(), catanh(), ccbrt(), and ComplexNumber::Mul().

{
    complex w;
    double a, b, c, d;

    // (a+bi)(c+di)
    a = creal(y);
    b = cimag(y);
    c = creal(z);
    d = cimag(z);

    // (ac -bd) + (ad + bc)i
    w = cpack(a * c - b * d, a * d + b * c);
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

conj()

complex conj

(

complex

z

)

Definition at line 59 of file prim.c.

References cpack().

Referenced by creci().

{
    IMAG_PART(z) = -IMAG_PART(z);
    return cpack(REAL_PART(z), IMAG_PART(z));
}

Here is the call graph for this function:

Here is the caller graph for this function:

cpack()

complex cpack	(	double	x,
		double	y
	)

Pack two real numbers into a complex number.

Definition at line 68 of file prim.c.

Referenced by ComplexNumber::Add(), cacos(), cacosh(), cacot(), cacoth(), cacsc(), cacsch(), cadd(), casec(), casech(), casin(), casinh(), catan(), catanh(), ccbrt(), cceil(), ccos(), ccosh(), ccot(), ccoth(), ccsc(), ccsch(), cdiv(), cexp(), cfloor(), clog(), clog10(), clogb(), cmul(), ComplexNumber::ComplexNumber(), conj(), cpow(), creci(), cround(), csec(), csech(), csin(), csinh(), csqrt(), csub(), ctan(), ctanh(), ctrunc(), ComplexNumber::Div(), ComplexNumber::Mul(), ComplexNumber::Raise(), ComplexNumber::Sub(), and ComplexNumber::Unary().

{
    complex z;

    REAL_PART(z) = x;
    IMAG_PART(z) = y;
    return (z);
}

Here is the caller graph for this function:

cpow()

complex cpow	(	complex	x,
		complex	z
	)

Complex number raised to a power.

Definition at line 42 of file cpow.c.

References atan2(), cabs(), cimag(), cos(), cpack(), creal(), exp(), log(), pow(), and sin().

Referenced by ComplexNumber::Raise().

{
    complex w;
    double x, y, r, theta, absa, arga;

    x = creal(z);
    y = cimag(z);
    absa = cabs(a);
    if (absa == 0.0)
    {
        return cpack(0.0, + 0.0);
    }
    arga = atan2(cimag(a), creal(a));

    r = pow(absa, x);
    theta = x * arga;
    if (y != 0.0)
    {
        r = r * exp(-y * arga);
        theta = theta + y * log(absa);
    }

    w = cpack(r * cos(theta), r * sin(theta));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

creal()

double creal

(

complex

z

)

Real part of complex number.

Definition at line 38 of file prim.c.

Referenced by cabs(), cadd(), cceil(), ccos(), ccosh(), ccot(), ccoth(), ccsc(), ccsch(), cdiv(), cexp(), cfloor(), clog(), cmul(), cpow(), creci(), cround(), csec(), csech(), csgn(), csin(), csinh(), csqrt(), csub(), ctan(), ctanh(), ctrunc(), ComplexNumber::GetDefaultPrecedence(), ComplexNumber::GetIntegerValue(), ComplexNumber::GetPrecedence(), ComplexNumber::GetRealValue(), DecimalSystem::GetText(), PositionalNumeralSystem::GetText(), ComplexNumber::IsInfinite(), ComplexNumber::IsNaN(), ComplexNumber::IsNegative(), ComplexNumber::IsZero(), ComplexNumber::Log(), ComplexNumber::Log10(), ComplexNumber::Log2(), ComplexNumber::PureComplexValue(), and ComplexNumber::Unary().

{
    return (REAL_PART(z));
}

Here is the caller graph for this function:

creci()

complex creci

(

complex

z

)

Reciprocal value of complex number.

Definition at line 181 of file prim.c.

References cimag(), conj(), cpack(), and creal().

Referenced by cacsch(), casec(), casech(), and ComplexNumber::Reciprocal().

{
    complex w;
    double q, a, b;

    a = creal(z);
    b = cimag(conj(z));
    q = a * a + b * b;
    w = cpack(a / q, b / q);

    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

cround()

complex cround

(

complex

z

)

Division of two complex numbers.

Definition at line 110 of file prim.c.

References cimag(), cpack(), creal(), and round().

Referenced by ComplexNumber::Round().

{
    complex w;
    w = cpack(round(creal(z)), round(cimag(z)));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

csec()

complex csec

(

complex

z

)

Secant of a complex number.

Calculated as in Open Office:
https://wiki.openoffice.org/wiki/Documentation/How_Tos/Calc:_IMSEC_function

a+bi
            2.0 * cos(a) * cosh(b)
real  = ---------------------------—
         cosh(2.0 * b) + cos(2.0 * a)

            2.0 * sin(a) * sinh(b)
imag  = ---------------------------—
         cosh(2.0 * b) + cos(2.0 * a)

Definition at line 48 of file csec.c.

References cimag(), cos(), cosh(), cpack(), creal(), sin(), and sinh().

Referenced by ComplexNumber::Secant().

{
    complex w;
    double a, b;
    double d;

    a = creal(z);
    b = cimag(z);
    d = cosh(2.0 * b) + cos(2.0 * a);

    if (d == 0.0)
    {
        w = cpack((double)INFP, (double)INFP);
    }
    else
    {
        w = cpack((2.0 * cos(a) * cosh(b) / d), (2.0 * sin(a) * sinh(b) / d));
    }

    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

csech()

complex csech

(

complex

z

)

Hyperbolic secant of a complex number.

Calculated as in Open Office:
https://wiki.openoffice.org/wiki/Documentation/How_Tos/Calc:_IMSECH_function

a+bi
            2.0 * cosh(a) * cos(b)
real  = ---------------------------—
         cosh(2.0 * a) + cos(2.0 * b)

        -2.0 * sinh(2.0 * a) * sin(b)
imag  = ---------------------------—
         cosh(2.0 * a) + cos(2.0 * b)

Definition at line 48 of file csech.c.

References cimag(), cos(), cosh(), cpack(), creal(), sin(), and sinh().

Referenced by ComplexNumber::HypSecant().

{
    complex w;
    double a, b;
    double d;

    a = creal(z);
    b = cimag(z);
    d = cosh(2.0 * a) + cos(2.0 * b);
    w = cpack((2.0 * cosh(a) * cos(b) / d), (-2.0 * sinh(a) * sin(b) / d));

    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

csgn()

double csgn

(

complex

z

)

Complex signum.

More info is available at Wikipedia:
https://wikipedia.org/wiki/Sign_function#Complex_signum

Definition at line 38 of file csgn.c.

References cimag(), and creal().

Referenced by ComplexNumber::Signum().

{
    double a = creal(z);

    if (a > 0.0)
    {
        return 1.0;
    }
    else if (a < 0.0)
    {
        return -1.0;
    }
    else
    {
        double b = cimag(z);
        return b > 0.0 ? 1.0 : b < 0.0 ? -1.0 : 0.0;
    }
}

Here is the call graph for this function:

Here is the caller graph for this function:

csin()

complex csin

(

complex

z

)

Sine of a complex number.

Calculated according to description at wikipedia:
https://wikipedia.org/wiki/Sine#Sine_with_a_complex_argument

a+bi
real = sin(a) * cosh(b)
imag = cos(a) * sinh(b)

Definition at line 50 of file csin.c.

References cchsh(), cimag(), cos(), cpack(), creal(), and sin().

Referenced by ComplexNumber::Sine().

{
    complex w;
    double a, b;
    double ch, sh;

    a = creal(z);
    b = cimag(z);
    cchsh(b, &ch, &sh);
    w = cpack((sin(a) * ch), (cos(a) * sh));

    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

csinh()

complex csinh

(

complex

z

)

Hyperbolic sine of a complex number.

Calculated as in Open Office:
https://wiki.openoffice.org/wiki/Documentation/How_Tos/Calc:_IMSINH_function

a+bi
real = sinh(a) * cos(b)
imag = cosh(a) * sin(b)

Definition at line 50 of file csinh.c.

References cchsh(), cimag(), cos(), cpack(), creal(), and sin().

Referenced by ComplexNumber::HypSine().

{
    complex w;
    double a, b;
    double ch, sh;

    a = creal(z);
    b = cimag(z);
    cchsh(a, &ch, &sh);
    w = cpack(cos(b) * sh, sin(b) * ch);

    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

csqrt()

complex csqrt

(

complex

z

)

Square root of complex number.

Definition at line 42 of file csqrt.c.

References cabs(), cimag(), cpack(), creal(), fabs(), and sqrt().

Referenced by cacos(), cacosh(), cacsc(), cacsch(), casec(), casech(), casin(), casinh(), and ComplexNumber::SquareRoot().

{
    complex w;
    double x, y, r, t, scale;

    x = creal(z);
    y = cimag(z);

    if (y == 0.0)
    {
        if (x == 0.0)
        {
            w = cpack(0.0, y);
        }
        else
        {
            r = fabs(x);
            r = sqrt(r);
            if (x < 0.0)
            {
                w = cpack(0.0, r);
            }
            else
            {
                w = cpack(r, y);
            }
        }
        return w;
    }
    if (x == 0.0)
    {
        r = fabs(y);
        r = sqrt(0.5 * r);
        if (y > 0)
            w = cpack(r, r);
        else
            w = cpack(r, -r);
        return w;
    }
    /* Rescale to avoid internal overflow or underflow.  */
    if ((fabs(x) > 4.0) || (fabs(y) > 4.0))
    {
        x *= 0.25;
        y *= 0.25;
        scale = 2.0;
    }
    else
    {
#if 1
        x *= 1.8014398509481984e16; /* 2^54 */
        y *= 1.8014398509481984e16;
        scale = 7.450580596923828125e-9; /* 2^-27 */
#else
        x *= 4.0;
        y *= 4.0;
        scale = 0.5;
#endif
    }
    w = cpack(x, y);
    r = cabs(w);
    if (x > 0)
    {
        t = sqrt(0.5 * r + 0.5 * x);
        r = scale * fabs((0.5 * y) / t);
        t *= scale;
    }
    else
    {
        r = sqrt(0.5 * r - 0.5 * x);
        t = scale * fabs((0.5 * y) / r);
        r *= scale;
    }
    if (y < 0)
        w = cpack(t, -r);
    else
        w = cpack(t, r);
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

csub()

complex csub	(	complex	a,
		complex	z
	)

Subtraction of two complex numbers.

Definition at line 130 of file prim.c.

References cimag(), cpack(), and creal().

Referenced by cacos(), cacosh(), cacot(), cacoth(), cacsc(), casec(), casech(), casin(), catan(), catanh(), and ComplexNumber::Sub().

{
    complex w;
    w = cpack(creal(y) - creal(z), cimag(y) - cimag(z));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

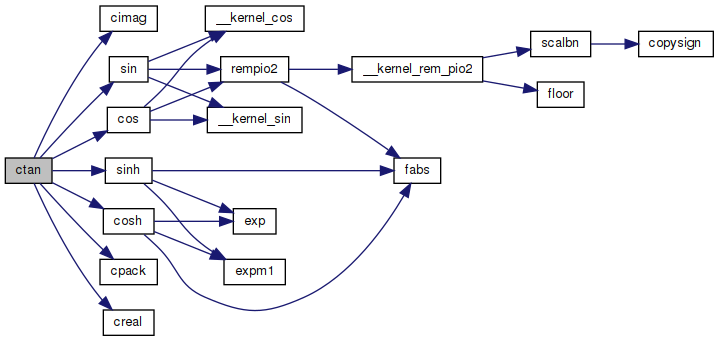
ctan()

complex ctan

(

complex

z

)

Tangent of a complex number.

Calculated as in Open Office:
https://wiki.openoffice.org/wiki/Documentation/How_Tos/Calc:_IMTAN_function

a+bi
               sin(2.0 * a)
real  = ---------------------------—
         cos(2.0 * a) + cosh(2.0 * b)
  sinh(2.0 * b)

imag  = ---------------------------—
         cos(2.0 * a) + cosh(2.0 * b)

Definition at line 55 of file ctan.c.

References cimag(), cos(), cosh(), cpack(), creal(), sin(), and sinh().

Referenced by ComplexNumber::Tangent().

{
    complex w;
    double a, b;
    double d;

    a = creal(z);
    b = cimag(z);
    d = cos(2.0 * a) + cosh(2.0 * b);

    if (d == 0.0)
    {
        w = cpack((double)INFP, (double)INFP);
    }
    else
    {
        w = cpack((sin(2.0 * a) / d), (sinh(2.0 * b) / d));
    }

    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

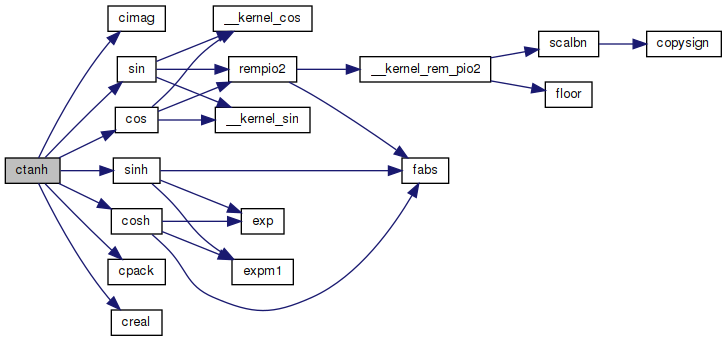
ctanh()

complex ctanh

(

complex

z

)

Hyperbolic tangent of a complex number.

a+bi
               sinh(2.0 * a)
real  = ---------------------------—
         cosh(2.0 * a) + cos(2.0 * b)
  sin(2.0 * b)

imag  = ---------------------------—
         cosh(2.0 * a) + cos(2.0 * b)

Definition at line 53 of file ctanh.c.

References cimag(), cos(), cosh(), cpack(), creal(), sin(), and sinh().

Referenced by ComplexNumber::HypTangent().

{
    complex w;
    double a, b;
    double d;

    a = creal(z);
    b = cimag(z);
    d = cosh(2.0 * a) + cos(2.0 * b);
    w = cpack((sinh(2.0 * a) / d), (sin(2.0 * b) / d));

    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function:

ctrunc()

complex ctrunc

(

complex

z

)

Truncated value of complex number.

Definition at line 80 of file prim.c.

References cimag(), cpack(), creal(), and trunc().

Referenced by ComplexNumber::Trunc().

{
    complex w;
    w = cpack(trunc(creal(z)), trunc(cimag(z)));
    return w;
}

Here is the call graph for this function:

Here is the caller graph for this function: