ComplexNumber Struct Reference

Represent a complex number with 2 components of 15 significant digits. More...

#include <cplex.h>

Inheritance diagram for ComplexNumber:

Collaboration diagram for ComplexNumber:

Public Member Functions
	ComplexNumber ()
	ComplexNumber (complex z)
	ComplexNumber (double real, double imag)
	~ComplexNumber ()
Number *	Clone ()
int	GetIntegerValue ()
double	GetRealValue ()
double	GetImagValue () const
complex	GetComplexValue () const
bool	PureComplexValue ()
int	GetPrecedence ()
int	GetDefaultPrecedence ()
bool	IsNegative ()
bool	IsZero ()
bool	IsNaN ()
	Returns true if number is NaN. More...
bool	IsInfinite ()
	Returns true if number is infinite. More...
bool	IsNotImplemented ()
Number *	Unary ()
Number *	Add (Number *other)
Number *	Sub (Number *other)
Number *	Mul (Number *other)
Number *	Div (Number *other)
Number *	Raise (Number *exponent)
Number *	Signum ()
Number *	Trunc ()
Number *	Round ()
Number *	Floor ()
Number *	Ceiling ()
Number *	Absolute ()
Number *	SquareRoot ()
Number *	CubeRoot ()
Number *	Reciprocal ()
Number *	Factorial ()
Number *	Log ()
Number *	Log2 ()
Number *	Log10 ()
Number *	Sine ()
Number *	Cosine ()
Number *	Tangent ()
Number *	Cosecant ()
Number *	Secant ()
Number *	Cotangent ()
Number *	Chord ()
Number *	ExSecant ()
Number *	ExCosecant ()
Number *	ArcSine ()
Number *	ArcCosine ()
Number *	ArcTangent ()
Number *	ArcCosecant ()
Number *	ArcSecant ()
Number *	ArcCotangent ()
Number *	ArcExSecant ()
Number *	ArcExCosecant ()
Number *	ArcChord ()
Number *	HypSine ()
Number *	HypCosine ()
Number *	HypTangent ()
Number *	HypCosecant ()
Number *	HypSecant ()
Number *	HypCotangent ()
Number *	HypArcSine ()
Number *	HypArcCosine ()
Number *	HypArcTangent ()
Number *	HypArcCosecant ()
Number *	HypArcSecant ()
Number *	HypArcCotangent ()
Number *	VerSine ()
Number *	VerCosine ()
Number *	CoVerSine ()
Number *	CoVerCosine ()
Number *	HaVerSine ()
Number *	HaVerCosine ()
Number *	HaCoVerSine ()
Number *	HaCoVerCosine ()
Number *	ArcVerSine ()
Number *	ArcVerCosine ()
Number *	ArcCoVerSine ()
Number *	ArcCoVerCosine ()
Number *	ArcHaVerSine ()
Number *	ArcHaVerCosine ()
Number *	ArcHaCoVerSine ()
Number *	ArcHaCoVerCosine ()
Public Member Functions inherited from Number
	Number (NumberSystem system)
virtual	~Number ()

Private Attributes
complex	z

Additional Inherited Members
Protected Attributes inherited from Number
NumberSystem	system

Detailed Description

Represent a complex number with 2 components of 15 significant digits.

Calculations are done using 64 bit IEEE 754 arithmetics.

Definition at line 46 of file cplex.h.

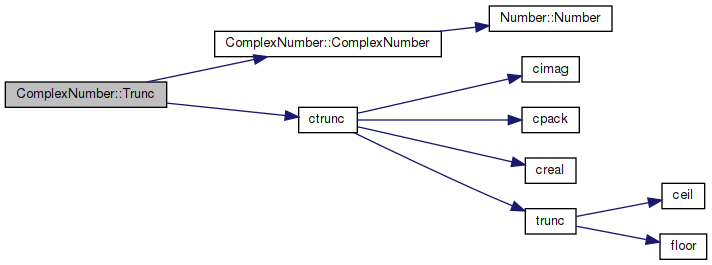
Constructor & Destructor Documentation

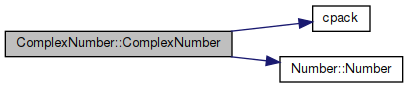
ComplexNumber() [1/3]

ComplexNumber::ComplexNumber

(

)

Definition at line 36 of file cplex.cpp.

References cpack(), nsyscomplex, Number::Number(), and z.

Referenced by Add(), Div(), Mul(), Raise(), and Sub().

                             : Number(nsyscomplex)
{
    z = cpack(0.0, 0.0);
}

Here is the call graph for this function:

Here is the caller graph for this function:

ComplexNumber() [2/3]

ComplexNumber::ComplexNumber ( complex  z )

explicit

Definition at line 41 of file cplex.cpp.

References nsyscomplex, Number::Number(), and z.

Referenced by Add(), ArcCosecant(), ArcCosine(), ArcCotangent(), ArcSecant(), ArcSine(), ArcTangent(), Ceiling(), Clone(), Cosecant(), Cosine(), Cotangent(), CubeRoot(), Div(), Floor(), HypArcCosecant(), HypArcCosine(), HypArcCotangent(), HypArcSecant(), HypArcSine(), HypArcTangent(), HypCosecant(), HypCosine(), HypCotangent(), HypSecant(), HypSine(), HypTangent(), Log(), Log10(), Log2(), Mul(), Raise(), Reciprocal(), Round(), Secant(), Sine(), SquareRoot(), Sub(), Tangent(), Trunc(), and Unary().

                                      : Number(nsyscomplex)
{
    this->z = z;
}

Here is the call graph for this function:

Here is the caller graph for this function:

ComplexNumber() [3/3]

ComplexNumber::ComplexNumber	(	double	real,
		double	imag
	)

Definition at line 46 of file cplex.cpp.

References cpack(), nsyscomplex, Number::Number(), and z.

Referenced by ComplexiNode::ComplexiNode(), RealNumber::CubeRoot(), RealNumber::Log(), RealNumber::Log10(), RealNumber::Log2(), Parser::ParseNumber(), RealNumber::Raise(), and RealNumber::SquareRoot().

                                                     : Number(nsyscomplex)
{
    z = cpack(real, imag);
}

Here is the call graph for this function:

Here is the caller graph for this function:

~ComplexNumber()

ComplexNumber::~ComplexNumber

(

)

Definition at line 51 of file cplex.cpp.

{
}

Member Function Documentation

Absolute()

Number * ComplexNumber::Absolute ( )

virtual

Implements Number.

Definition at line 280 of file cplex.cpp.

References cabs(), RealNumber::RealNumber(), and z.

{
    return new RealNumber(cabs(z));
}

Here is the call graph for this function:

Add()

Number * ComplexNumber::Add ( Number *  other )

virtual

Implements Number.

Definition at line 170 of file cplex.cpp.

References cadd(), ComplexNumber(), cpack(), Number::IsNaN(), nnnan, NonNumber::NonNumber(), nsyscomplex, nsysreal, Number::system, RealNumber::x, and z.

{
    if (other->IsNaN())
        return new NonNumber(nnnan);

    if (other->system == nsyscomplex)
    {
        ComplexNumber *w = static_cast<ComplexNumber *>(other);
        return new ComplexNumber(cadd(z, w->z));
    }

    if (other->system == nsysreal)
    {
        RealNumber *a = static_cast<RealNumber *>(other);
        return new ComplexNumber(cadd(z, cpack(a->x, 0.0)));
    }

    return new ComplexNumber();
}

Here is the call graph for this function:

ArcChord()

Number * ComplexNumber::ArcChord ( )

virtual

Implements Number.

Definition at line 419 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

ArcCosecant()

Number * ComplexNumber::ArcCosecant ( )

virtual

Implements Number.

Definition at line 409 of file cplex.cpp.

References cacsc(), ComplexNumber(), and z.

{
    return new ComplexNumber(cacsc(z));
}

Here is the call graph for this function:

ArcCosine()

Number * ComplexNumber::ArcCosine ( )

virtual

Implements Number.

Definition at line 394 of file cplex.cpp.

References cacos(), ComplexNumber(), and z.

{
    return new ComplexNumber(cacos(z));
}

Here is the call graph for this function:

ArcCotangent()

Number * ComplexNumber::ArcCotangent ( )

virtual

Implements Number.

Definition at line 414 of file cplex.cpp.

References cacot(), ComplexNumber(), and z.

{
    return new ComplexNumber(cacot(z));
}

Here is the call graph for this function:

ArcCoVerCosine()

Number * ComplexNumber::ArcCoVerCosine ( )

virtual

Implements Number.

Definition at line 549 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

ArcCoVerSine()

Number * ComplexNumber::ArcCoVerSine ( )

virtual

Implements Number.

Definition at line 544 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

ArcExCosecant()

Number * ComplexNumber::ArcExCosecant ( )

virtual

Implements Number.

Definition at line 429 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

ArcExSecant()

Number * ComplexNumber::ArcExSecant ( )

virtual

Implements Number.

Definition at line 424 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

ArcHaCoVerCosine()

Number * ComplexNumber::ArcHaCoVerCosine ( )

virtual

Implements Number.

Definition at line 569 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

ArcHaCoVerSine()

Number * ComplexNumber::ArcHaCoVerSine ( )

virtual

Implements Number.

Definition at line 564 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

ArcHaVerCosine()

Number * ComplexNumber::ArcHaVerCosine ( )

virtual

Implements Number.

Definition at line 559 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

ArcHaVerSine()

Number * ComplexNumber::ArcHaVerSine ( )

virtual

Implements Number.

Definition at line 554 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

ArcSecant()

Number * ComplexNumber::ArcSecant ( )

virtual

Implements Number.

Definition at line 404 of file cplex.cpp.

References casec(), ComplexNumber(), and z.

{
    return new ComplexNumber(casec(z));
}

Here is the call graph for this function:

ArcSine()

Number * ComplexNumber::ArcSine ( )

virtual

Implements Number.

Definition at line 389 of file cplex.cpp.

References casin(), ComplexNumber(), and z.

{
    return new ComplexNumber(casin(z));
}

Here is the call graph for this function:

ArcTangent()

Number * ComplexNumber::ArcTangent ( )

virtual

Implements Number.

Definition at line 399 of file cplex.cpp.

References catan(), ComplexNumber(), and z.

{
    return new ComplexNumber(catan(z));
}

Here is the call graph for this function:

ArcVerCosine()

Number * ComplexNumber::ArcVerCosine ( )

virtual

Implements Number.

Definition at line 539 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

ArcVerSine()

Number * ComplexNumber::ArcVerSine ( )

virtual

Implements Number.

Definition at line 534 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

Ceiling()

Number * ComplexNumber::Ceiling ( )

virtual

Implements Number.

Definition at line 300 of file cplex.cpp.

References cceil(), ComplexNumber(), and z.

{
    return new ComplexNumber(cceil(z));
}

Here is the call graph for this function:

Chord()

Number * ComplexNumber::Chord ( )

virtual

Implements Number.

Definition at line 374 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

Clone()

Number * ComplexNumber::Clone ( )

virtual

Implements Number.

Definition at line 55 of file cplex.cpp.

References ComplexNumber(), and z.

{
    return new ComplexNumber(z);
}

Here is the call graph for this function:

Cosecant()

Number * ComplexNumber::Cosecant ( )

virtual

Implements Number.

Definition at line 364 of file cplex.cpp.

References ccsc(), ComplexNumber(), and z.

{
    return new ComplexNumber(ccsc(z));
}

Here is the call graph for this function:

Cosine()

Number * ComplexNumber::Cosine ( )

virtual

Implements Number.

Definition at line 349 of file cplex.cpp.

References ccos(), ComplexNumber(), and z.

{
    return new ComplexNumber(ccos(z));
}

Here is the call graph for this function:

Cotangent()

Number * ComplexNumber::Cotangent ( )

virtual

Implements Number.

Definition at line 369 of file cplex.cpp.

References ccot(), ComplexNumber(), and z.

{
    return new ComplexNumber(ccot(z));
}

Here is the call graph for this function:

CoVerCosine()

Number * ComplexNumber::CoVerCosine ( )

virtual

Implements Number.

Definition at line 509 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

CoVerSine()

Number * ComplexNumber::CoVerSine ( )

virtual

Implements Number.

Definition at line 504 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

CubeRoot()

Number * ComplexNumber::CubeRoot ( )

virtual

Implements Number.

Definition at line 315 of file cplex.cpp.

References ccbrt(), ComplexNumber(), and z.

{
    return new ComplexNumber(ccbrt(z));
}

Here is the call graph for this function:

Div()

Number * ComplexNumber::Div ( Number *  other )

virtual

Implements Number.

Definition at line 230 of file cplex.cpp.

References cdiv(), ComplexNumber(), cpack(), Number::IsNaN(), Number::IsZero(), nnnan, NonNumber::NonNumber(), nsyscomplex, nsysreal, Number::system, RealNumber::x, and z.

{
    if (other->IsZero() || other->IsNaN())
        return new NonNumber(nnnan);

    if (other->system == nsyscomplex)
    {
        ComplexNumber *w = static_cast<ComplexNumber *>(other);
        return new ComplexNumber(cdiv(z, w->z));
    }

    if (other->system == nsysreal)
    {
        RealNumber *a = static_cast<RealNumber *>(other);
        return new ComplexNumber(cdiv(z, cpack(a->x, 0.0)));
    }

    return new ComplexNumber();
}

Here is the call graph for this function:

ExCosecant()

Number * ComplexNumber::ExCosecant ( )

virtual

Implements Number.

Definition at line 384 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

ExSecant()

Number * ComplexNumber::ExSecant ( )

virtual

Implements Number.

Definition at line 379 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

Factorial()

Number * ComplexNumber::Factorial ( )

virtual

Implements Number.

Definition at line 270 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

Floor()

Number * ComplexNumber::Floor ( )

virtual

Implements Number.

Definition at line 295 of file cplex.cpp.

References cfloor(), ComplexNumber(), and z.

{
    return new ComplexNumber(cfloor(z));
}

Here is the call graph for this function:

GetComplexValue()

complex ComplexNumber::GetComplexValue

(

)

const

Definition at line 75 of file cplex.cpp.

References z.

Referenced by DecimalSystem::GetText(), and PositionalNumeralSystem::GetText().

{
    return z;
}

Here is the caller graph for this function:

GetDefaultPrecedence()

int ComplexNumber::GetDefaultPrecedence ( )

virtual

Implements Number.

Definition at line 101 of file cplex.cpp.

References cimag(), creal(), and z.

{
    return (creal(z) != 0.0 && cimag(z) != 0.0) ? 2 : 0;
}

Here is the call graph for this function:

GetImagValue()

double ComplexNumber::GetImagValue

(

)

const

Definition at line 70 of file cplex.cpp.

References cimag(), and z.

{
    return cimag(z);
}

Here is the call graph for this function:

GetIntegerValue()

int ComplexNumber::GetIntegerValue ( )

virtual

Implements Number.

Definition at line 60 of file cplex.cpp.

References creal(), and z.

{
    return static_cast<int>(creal(z));
}

Here is the call graph for this function:

GetPrecedence()

int ComplexNumber::GetPrecedence ( )

virtual

Implements Number.

Definition at line 85 of file cplex.cpp.

References cimag(), creal(), and z.

{
    if ((creal(z) < 0.0) || (creal(z) == 0.0 && cimag(z) < 0.0))
    {
        return -1;
    }
    else if (creal(z) != 0.0 && cimag(z) != 0.0)
    {
        return 2;
    }
    else
    {
        return 0;
    }
}

Here is the call graph for this function:

GetRealValue()

double ComplexNumber::GetRealValue ( )

virtual

Implements Number.

Definition at line 65 of file cplex.cpp.

References creal(), and z.

{
    return creal(z);
}

Here is the call graph for this function:

HaCoVerCosine()

Number * ComplexNumber::HaCoVerCosine ( )

virtual

Implements Number.

Definition at line 529 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

HaCoVerSine()

Number * ComplexNumber::HaCoVerSine ( )

virtual

Implements Number.

Definition at line 524 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

HaVerCosine()

Number * ComplexNumber::HaVerCosine ( )

virtual

Implements Number.

Definition at line 519 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

HaVerSine()

Number * ComplexNumber::HaVerSine ( )

virtual

Implements Number.

Definition at line 514 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

HypArcCosecant()

Number * ComplexNumber::HypArcCosecant ( )

virtual

Implements Number.

Definition at line 484 of file cplex.cpp.

References cacsch(), ComplexNumber(), and z.

{
    return new ComplexNumber(cacsch(z));
}

Here is the call graph for this function:

HypArcCosine()

Number * ComplexNumber::HypArcCosine ( )

virtual

Implements Number.

Definition at line 469 of file cplex.cpp.

References cacosh(), ComplexNumber(), and z.

{
    return new ComplexNumber(cacosh(z));
}

Here is the call graph for this function:

HypArcCotangent()

Number * ComplexNumber::HypArcCotangent ( )

virtual

Implements Number.

Definition at line 489 of file cplex.cpp.

References cacoth(), ComplexNumber(), and z.

{
    return new ComplexNumber(cacoth(z));
}

Here is the call graph for this function:

HypArcSecant()

Number * ComplexNumber::HypArcSecant ( )

virtual

Implements Number.

Definition at line 479 of file cplex.cpp.

References casech(), ComplexNumber(), and z.

{
    return new ComplexNumber(casech(z));
}

Here is the call graph for this function:

HypArcSine()

Number * ComplexNumber::HypArcSine ( )

virtual

Implements Number.

Definition at line 464 of file cplex.cpp.

References casinh(), ComplexNumber(), and z.

{
    return new ComplexNumber(casinh(z));
}

Here is the call graph for this function:

HypArcTangent()

Number * ComplexNumber::HypArcTangent ( )

virtual

Implements Number.

Definition at line 474 of file cplex.cpp.

References catanh(), ComplexNumber(), and z.

{
    return new ComplexNumber(catanh(z));
}

Here is the call graph for this function:

HypCosecant()

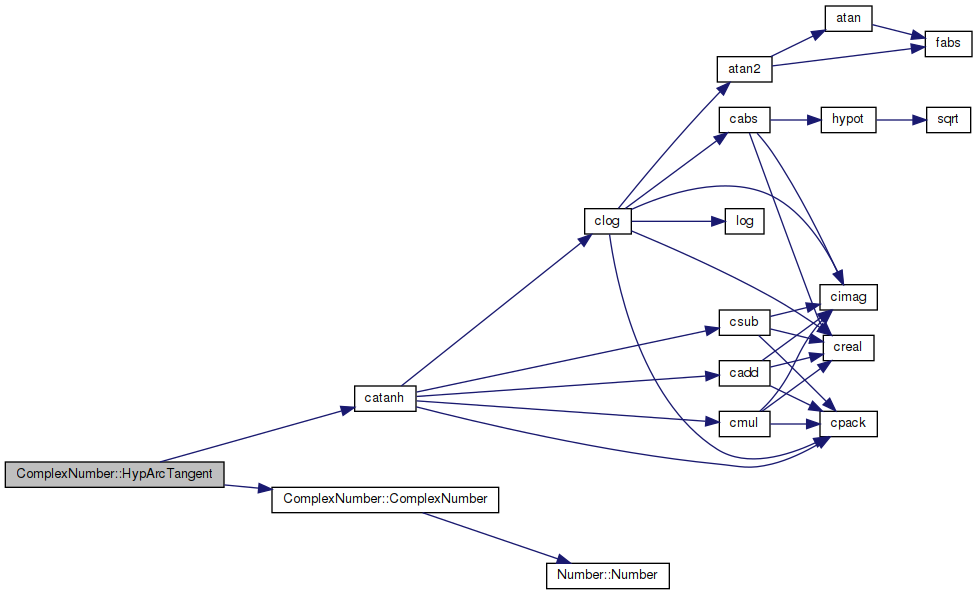
Number * ComplexNumber::HypCosecant ( )

virtual

Implements Number.

Definition at line 454 of file cplex.cpp.

References ccsch(), ComplexNumber(), and z.

{
    return new ComplexNumber(ccsch(z));
}

Here is the call graph for this function:

HypCosine()

Number * ComplexNumber::HypCosine ( )

virtual

Implements Number.

Definition at line 439 of file cplex.cpp.

References ccosh(), ComplexNumber(), and z.

{
    return new ComplexNumber(ccosh(z));
}

Here is the call graph for this function:

HypCotangent()

Number * ComplexNumber::HypCotangent ( )

virtual

Implements Number.

Definition at line 459 of file cplex.cpp.

References ccoth(), ComplexNumber(), and z.

{
    return new ComplexNumber(ccoth(z));
}

Here is the call graph for this function:

HypSecant()

Number * ComplexNumber::HypSecant ( )

virtual

Implements Number.

Definition at line 449 of file cplex.cpp.

References ComplexNumber(), csech(), and z.

{
    return new ComplexNumber(csech(z));
}

Here is the call graph for this function:

HypSine()

Number * ComplexNumber::HypSine ( )

virtual

Implements Number.

Definition at line 434 of file cplex.cpp.

References ComplexNumber(), csinh(), and z.

{
    return new ComplexNumber(csinh(z));
}

Here is the call graph for this function:

HypTangent()

Number * ComplexNumber::HypTangent ( )

virtual

Implements Number.

Definition at line 444 of file cplex.cpp.

References ComplexNumber(), ctanh(), and z.

{
    return new ComplexNumber(ctanh(z));
}

Here is the call graph for this function:

IsInfinite()

bool ComplexNumber::IsInfinite ( )

virtual

Returns true if number is infinite.

Implements Number.

Definition at line 136 of file cplex.cpp.

References cimag(), creal(), FloatUnion64::floatingPoint, FloatUnion64::IsInf(), FloatUnion64::IsMaxNegative(), FloatUnion64::IsMaxPositive(), and z.

{
    double a = creal(z);
    double b = cimag(z);

    // Handle subnormal values
    bool subInf = 
        (a > 0 && a <= 1e-308) || (a < 0 && a >= -1e-308) ||
        (b > 0 && b <= 1e-308) || (b < 0 && b >= -1e-308);

    if (subInf)
    {
        return true;
    }

    FloatUnion64 d, e;
    d.floatingPoint = a;
    e.floatingPoint = b;
    return d.IsInf() || e.IsInf() ||
           d.IsMaxPositive() || d.IsMaxNegative() ||
           e.IsMaxPositive() || e.IsMaxNegative();
}

Here is the call graph for this function:

IsNaN()

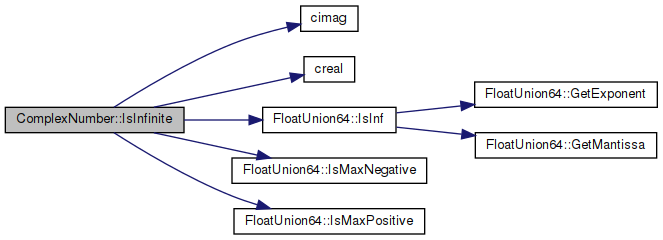
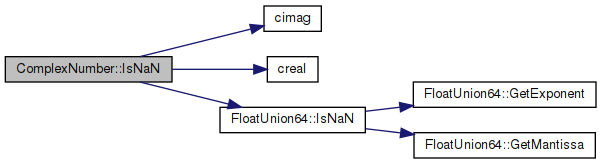
bool ComplexNumber::IsNaN ( )

virtual

Returns true if number is NaN.

Implements Number.

Definition at line 125 of file cplex.cpp.

References cimag(), creal(), FloatUnion64::floatingPoint, FloatUnion64::IsNaN(), and z.

{
    FloatUnion64 d, e;
    d.floatingPoint = creal(z);
    e.floatingPoint = cimag(z);
    return d.IsNaN() || e.IsNaN();
}

Here is the call graph for this function:

IsNegative()

bool ComplexNumber::IsNegative ( )

virtual

Implements Number.

Definition at line 106 of file cplex.cpp.

References cimag(), creal(), FloatUnion64::floatingPoint, FloatUnion64::IsNegative(), and z.

{
    FloatUnion64 d, e;
    d.floatingPoint = creal(z);
    e.floatingPoint = cimag(z);
    return d.IsNegative() && e.IsNegative();
}

Here is the call graph for this function:

IsNotImplemented()

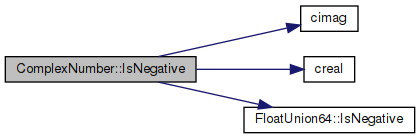
bool ComplexNumber::IsNotImplemented ( )

virtual

Implements Number.

Definition at line 159 of file cplex.cpp.

{
    return false;
}

IsZero()

bool ComplexNumber::IsZero ( )

virtual

Implements Number.

Definition at line 114 of file cplex.cpp.

References cimag(), creal(), FloatUnion64::floatingPoint, FloatUnion64::IsZero(), and z.

{
    FloatUnion64 d, e;
    d.floatingPoint = creal(z);
    e.floatingPoint = cimag(z);
    return d.IsZero() && e.IsZero();
}

Here is the call graph for this function:

Log()

Number * ComplexNumber::Log ( )

virtual

Implements Number.

Definition at line 320 of file cplex.cpp.

References cimag(), clog(), ComplexNumber(), creal(), nnnan, NonNumber::NonNumber(), and z.

{
    if (creal(z) == 0.0 && cimag(z) == 0.0)
        return new NonNumber(nnnan);

    return new ComplexNumber(clog(z));
}

Here is the call graph for this function:

Log10()

Number * ComplexNumber::Log10 ( )

virtual

Implements Number.

Definition at line 336 of file cplex.cpp.

References cimag(), clog10(), ComplexNumber(), creal(), nnnan, NonNumber::NonNumber(), and z.

{
    if (creal(z) == 0.0 && cimag(z) == 0.0)
        return new NonNumber(nnnan);

    return new ComplexNumber(clog10(z));
}

Here is the call graph for this function:

Log2()

Number * ComplexNumber::Log2 ( )

virtual

Implements Number.

Definition at line 328 of file cplex.cpp.

References cimag(), clogb(), ComplexNumber(), creal(), nnnan, NonNumber::NonNumber(), and z.

{
    if (creal(z) == 0.0 && cimag(z) == 0.0)
        return new NonNumber(nnnan);

    return new ComplexNumber(clogb(z));
}

Here is the call graph for this function:

Mul()

Number * ComplexNumber::Mul ( Number *  other )

virtual

Implements Number.

Definition at line 210 of file cplex.cpp.

References cmul(), ComplexNumber(), cpack(), Number::IsNaN(), nnnan, NonNumber::NonNumber(), nsyscomplex, nsysreal, Number::system, RealNumber::x, and z.

{
    if (other->IsNaN())
        return new NonNumber(nnnan);

    if (other->system == nsyscomplex)
    {
        ComplexNumber *w = static_cast<ComplexNumber *>(other);
        return new ComplexNumber(cmul(z, w->z));
    }

    if (other->system == nsysreal)
    {
        RealNumber *a = static_cast<RealNumber *>(other);
        return new ComplexNumber(cmul(z, cpack(a->x, 0.0)));
    }

    return new ComplexNumber();
}

Here is the call graph for this function:

PureComplexValue()

bool ComplexNumber::PureComplexValue ( )

virtual

Implements Number.

Definition at line 80 of file cplex.cpp.

References creal(), and z.

{
    return (creal(z) == 0.0);
}

Here is the call graph for this function:

Raise()

Number * ComplexNumber::Raise ( Number *  exponent )

virtual

Implements Number.

Definition at line 250 of file cplex.cpp.

References ComplexNumber(), cpack(), cpow(), Number::IsNaN(), nnnan, NonNumber::NonNumber(), nsyscomplex, nsysreal, Number::system, RealNumber::x, and z.

Referenced by RealNumber::Raise().

{
    if (exponent->IsNaN())
        return new NonNumber(nnnan);

    if (exponent->system == nsyscomplex)
    {
        ComplexNumber *w = static_cast<ComplexNumber *>(exponent);
        return new ComplexNumber(cpow(z, w->z));
    }

    if (exponent->system == nsysreal)
    {
        RealNumber *a = static_cast<RealNumber *>(exponent);
        return new ComplexNumber(cpow(z, cpack(a->x, 0.0)));
    }

    return new ComplexNumber();
}

Here is the call graph for this function:

Here is the caller graph for this function:

Reciprocal()

Number * ComplexNumber::Reciprocal ( )

virtual

Implements Number.

Definition at line 310 of file cplex.cpp.

References ComplexNumber(), creci(), and z.

{
    return new ComplexNumber(creci(z));
}

Here is the call graph for this function:

Round()

Number * ComplexNumber::Round ( )

virtual

Implements Number.

Definition at line 290 of file cplex.cpp.

References ComplexNumber(), cround(), and z.

{
    return new ComplexNumber(cround(z));
}

Here is the call graph for this function:

Secant()

Number * ComplexNumber::Secant ( )

virtual

Implements Number.

Definition at line 359 of file cplex.cpp.

References ComplexNumber(), csec(), and z.

{
    return new ComplexNumber(csec(z));
}

Here is the call graph for this function:

Signum()

Number * ComplexNumber::Signum ( )

virtual

Implements Number.

Definition at line 275 of file cplex.cpp.

References csgn(), RealNumber::RealNumber(), and z.

{
    return new RealNumber(csgn(z));
}

Here is the call graph for this function:

Sine()

Number * ComplexNumber::Sine ( )

virtual

Implements Number.

Definition at line 344 of file cplex.cpp.

References ComplexNumber(), csin(), and z.

{
    return new ComplexNumber(csin(z));
}

Here is the call graph for this function:

SquareRoot()

Number * ComplexNumber::SquareRoot ( )

virtual

Implements Number.

Definition at line 305 of file cplex.cpp.

References ComplexNumber(), csqrt(), and z.

{
    return new ComplexNumber(csqrt(z));
}

Here is the call graph for this function:

Sub()

Number * ComplexNumber::Sub ( Number *  other )

virtual

Implements Number.

Definition at line 190 of file cplex.cpp.

References ComplexNumber(), cpack(), csub(), Number::IsNaN(), nnnan, NonNumber::NonNumber(), nsyscomplex, nsysreal, Number::system, RealNumber::x, and z.

{
    if (other->IsNaN())
        return new NonNumber(nnnan);

    if (other->system == nsyscomplex)
    {
        ComplexNumber *w = static_cast<ComplexNumber *>(other);
        return new ComplexNumber(csub(z, w->z));
    }

    if (other->system == nsysreal)
    {
        RealNumber *a = static_cast<RealNumber *>(other);
        return new ComplexNumber(csub(z, cpack(a->x, 0.0)));
    }

    return new ComplexNumber();
}

Here is the call graph for this function:

Tangent()

Number * ComplexNumber::Tangent ( )

virtual

Implements Number.

Definition at line 354 of file cplex.cpp.

References ComplexNumber(), ctan(), and z.

{
    return new ComplexNumber(ctan(z));
}

Here is the call graph for this function:

Trunc()

Number * ComplexNumber::Trunc ( )

virtual

Implements Number.

Definition at line 285 of file cplex.cpp.

References ComplexNumber(), ctrunc(), and z.

{
    return new ComplexNumber(ctrunc(z));
}

Here is the call graph for this function:

Unary()

Number * ComplexNumber::Unary ( )

virtual

Implements Number.

Definition at line 164 of file cplex.cpp.

References cimag(), ComplexNumber(), cpack(), creal(), and z.

{
    complex w = cpack(-creal(z), -cimag(z));
    return new ComplexNumber(w);
}

Here is the call graph for this function:

VerCosine()

Number * ComplexNumber::VerCosine ( )

virtual

Implements Number.

Definition at line 499 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

VerSine()

Number * ComplexNumber::VerSine ( )

virtual

Implements Number.

Definition at line 494 of file cplex.cpp.

References nnnimp, and NonNumber::NonNumber().

{
    return new NonNumber(nnnimp);
}

Here is the call graph for this function:

Member Data Documentation

z

complex ComplexNumber::z

private

Definition at line 141 of file cplex.h.

Referenced by Absolute(), Add(), ArcCosecant(), ArcCosine(), ArcCotangent(), ArcSecant(), ArcSine(), ArcTangent(), Ceiling(), Clone(), ComplexNumber(), Cosecant(), Cosine(), Cotangent(), CubeRoot(), Div(), Floor(), GetComplexValue(), GetDefaultPrecedence(), GetImagValue(), GetIntegerValue(), GetPrecedence(), GetRealValue(), HypArcCosecant(), HypArcCosine(), HypArcCotangent(), HypArcSecant(), HypArcSine(), HypArcTangent(), HypCosecant(), HypCosine(), HypCotangent(), HypSecant(), HypSine(), HypTangent(), IsInfinite(), IsNaN(), IsNegative(), IsZero(), Log(), Log10(), Log2(), Mul(), PureComplexValue(), Raise(), Reciprocal(), Round(), Secant(), Signum(), Sine(), SquareRoot(), Sub(), Tangent(), Trunc(), and Unary().

---

The documentation for this struct was generated from the following files:

• src/lib/cplex.h
• src/lib/cplex.cpp